考研数据结构与算法(四)字符串¶
一、基本概念¶
串(String)是由零个或多个字符组成的有限序列。一般记为:
其中 \(S\) 是串名,单引号括起来的字符串序列是串的值, \(a_i\) 可以是字母、数字、或者其他字符,串中的 \(n\) 代表的是串的长度,当 \(n=0\) 时,称其为空串
串的逻辑结构和线性表极为相似,区别仅在于串的数据对象限定在字符集中,在基本操作上也有很大的区别,例如线性表的操作通常是单个元素的操作,而串的操作是以子串(子串的大小是不确定的)为操作对象。
1.1 主串和字串¶
串中任意个连续的字符组成的子序列称为该串的 子串 。包含字串的串则称为该子串的 主串
例如,假设有一字串 abb 那么它的 主串 可以是 aabbb 也可以是 abbbc 或者其他任何包含该子串的串
1.2 串的操作函数¶
| 串的操作函数 | 作用 |
|---|---|
Concat(&T,S1,S2) |
将字符串 \(S1\) 和 \(S2\) 连接并复制给 \(T\) 串 |
SubString(&Sub,S,pos,len) |
将字符串 \(S\) 从 \(pos\) 到 \(pos+len\) 的子串取出并赋值给 \(Sub\) 串 |
StrCopy(&T,S) |
将字符串 \(S\) 的值复制给字符串 \(T\) |
StrLength(S) |
求字符串 \(S\) 的长度 |
Index(S,T) |
如果 \(S\) 中存在子串 \(T\) 则返回第一次出现的位置,否则返回 \(0\) |
二、存储结构¶
2.1 定长顺序存储¶
和线性表的顺序存储结构相同,用一组连续的空间存储字符序列,结构如下:
#define MAXLEN 255
typedef struct {
char ch[MAXLEN];
int length;
}SString;
串的长度最多能为 MAXLEN 但是考虑到字符串以 \(\0\) 结尾,也就是需要给字符串结束标识符留一个位置,那么实际的串长为 MAXLEN-1 但是由于我们这里设计该字符串结构的时候有一个 length 表示,所以我们可以使用到完整的 MAXLEN 的长度
2.2 堆分配存储¶
堆分配存储表示仍然以一组地址连续的存储单元存放串值的字符序列 ,但它们的存储空间是在程序执行过程中 动态分配 得到的,结构如下:
typedef struct {
char *ch;
int length;
}SString;
我们在堆的这个自由存储区去定制话分配空间,在C语言中,通过 malloc 和 free 函数可以完成动态存储管理。利用 malloc )为每个新产生的串分配一块实际串长所需的存储空间,若分配成功则会返回一个指向分配空间起始地址的一个指针,作为字符串的基地址,我们则可以通过 ch 指针来访问这块空间,若分配失败,则返回 NULL 。
当然这里通过堆分配存储的话,需要我们自动管理内存,所以每当我们 malloc 了一个空间,我们需要在合适的地方去 free 掉,不然申请的空间越来越多最后就会没有空间可以使用,造成内存泄漏
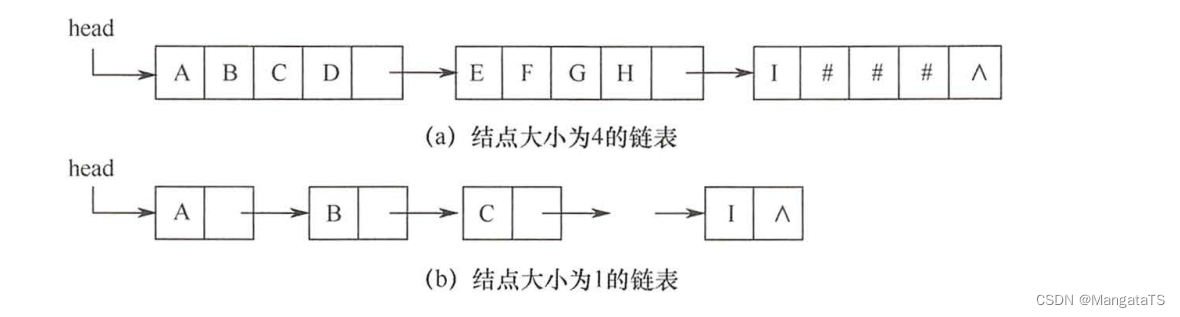
2.3 块链存储¶
这个就类似线性表的链式存储,不同的是对于每一个单元结点我们都将其当作一个定长字符串也就是一个块,那么不难得出如下结构:
#define MAXLEN 255
typedef struct SString{
char ch[MAXLEN];
struct SString * next;
}SString;
当然如果对于每一块的长度不定的话,我们同样可以通过堆空间的分配来做
#define MAXLEN 255
typedef struct SString{
char *ch;
int length;
struct SString * next;
}SString;
那么可以想象到这个结构:
三、串的匹配算法¶
在串 \(S\) 中找到子串 \(T\) 第一次出现的位置,如果没找到则返回 \(-1\)
3.1 暴力匹配¶
我们将串 \(T\) 不断的从串 \(S\) 的第一个位置往后一一比较,如果匹配失败则整体往后移动一位,操作如下图所示:

不难得出代码:
int Index(SString S,SString T) {
for(int i = 0,len = S.length - T.length + 1;i < len; ++i) {
bool fg = true;
for(int j = 0;j < T.length; ++j) {
if(S.ch[i] != T.ch[j]) {//匹配失败
fg = false;//将当前位置的匹配flag标为失败
break;
}
}
if(fg) return i;
}
return -1;//如果发现没有匹配成功则返回-1
}
3.2 KMP匹配¶
详情可以参考我的这一篇博客:
https://acmer.blog.csdn.net/article/details/118560016
我这里再着重讲一下 \(next\) 数组和 \(nextval\) 数组
3.2.1 next数组¶
通过上面的描述我们大概知道了 \(next\) 数组其实是表示的前一个子串的状态,例如如果有 \(next[i]\) 那么这个表示的是从 \(0\) 到 \(i-1\) 这部分串构成的子串的PM匹配值,也就是我们讲的最长公共前后缀
已知道我们进行匹配的时候如果发生不匹配的情况的话,我们并不是回溯,而是让 \(i\) 指针不动, 而串 \(T\) 整体右移一定长度,然后此时将 \(j\) 跳到上一个匹配位置。
右移位数=已匹配的字符数-对应的部分匹配值,即:\(Move = (j-1) -PM[j-1]\) 那么我们如果将 \(PM\) 整体右移一位然后左端用 \(-1\) 补齐的话,我们就会发现: \(Move = (j-1) -Next[j]\)
例如有字符串 abcac 的 \(PM\) 表和 \(Next\) 表
| 编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| S | a | b | c | a | c |
| PM | 0 | 0 | 0 | 1 | 0 |
| Next | -1 | 0 | 0 | 0 | 1 |
我们可以注意到:
- 第一个元素右移后左端的空白用 \(-1\) 补充,这样的话如果是第一个元素匹配失败,则子串将整体右移一位
- 最后一个元素的PM值其实没有什么作用,所以可以舍去
这样如果发生失配要回退的时候就为:
所以有的时候为了让公式更加简洁,则将 \(Next\) 数组所有元素整体加一,于是上面字符串 abcac 的Next表可以写成这样:
| 编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| S | a | b | c | a | c |
| PM | 0 | 0 | 0 | 1 | 0 |
| Next | 0 | 1 | 1 | 1 | 2 |
于是可以得到简单的实现:
void get_next(String T) {
int i = 0,j = -1;
nextt[0] = -1;
while(i < T.length) {
if(j == -1 || T[i] == T[j]) nextt[++i] = ++j;
else j = nextt[j];
}
}
int kmp(String S,String T) {
int i = 0,j = 0;
get_next();
while(i < S.length) {
if(j == -1 || T[j] == S[i]) ++i,++j;
else j = nextt[j];
if(j == T.length) return i-T.length;
}
return -1;
}
3.2.2 NextVal数组¶
这个其实是上面KMP算法中提到的匹配优化,例如串 \(T\) aaaab 和主串 \(S\) aaabaaaab 进行匹配的时候:
| 主串S | a | a | a | b | a | a | a | a | b |
|---|---|---|---|---|---|---|---|---|---|
| 模式串T | a | a | a | a | b | ||||
| j | 1 | 2 | 3 | 4 | 5 | ||||
| \(Next[j]\) | 0 | 1 | 2 | 3 | 4 | ||||
| \(Nextval[j]\) | 0 | 0 | 0 | 0 | 4 |
我们可以看到当 \(i = 4 ,j = 4\) 的时候发生了匹配失败,如果是按照之前的 \(Move\) 操作的话,我们会发现,会进行 \(S[4]\) 和 \(T[3]\) 匹配,然后 \(S[4]\) 和 \(T[2]\) 匹配,最后和 \(T[1]\) 匹配,实际上我们会发现,这样匹配下去是没有意义的,因为一定会匹配失败,因为我们每次都是拿了一个和 \(T[4]\) 相同的元素进行匹配,这样一定会发生失败,所以我们有了 \(Nextval\) 数组,让我们每次匹配的字符和上一个不同的位置,这个也就是我们上面讲到的压缩路径,于是不难得到 get_next 代码:
void get_next(String S) {
int i = 0,j = -1;
nextt[0] = -1;//这个是辅助计算next值得
while(i < S.length) {
if(j == -1 || S[i] == S[j]) {
++i,++j;
if(S[i] == S[j]) nextt[j] = next[i];//压缩路径
else nextt[i] = j;
}
else j = nextt[j]; //否则j进行回溯
}
}