
最短路¶
前言¶
如果你对图论相关知识一点也没有,那么建议您先去了解这些知识:https://acmer.blog.csdn.net/article/details/122310835,然后就可以快乐的学习最短路算法啦
视频中绘图软件:https://csacademy.com/app/graph_editor/
配套讲解视频:https://www.bilibili.com/video/BV1Fa411C7wX/
如果哪里讲的有问题欢迎在评论区指出,感谢支持!
一、Floyd算法¶
1.1简介¶
Floyd算法算是最简单的算法,没有之一。适用于任何图
不管有向无向,边权正负,但是最短路必须存在。
基于动态规划的思想
1.2复杂度¶
1.2.1时间复杂度¶
\(O(N^3)\)
1.2.2空间复杂度¶
\(O(N^2)\)
1.3优缺点¶
1.3.1优点¶
常数小, 容易实现 ,思路简单,能处理大部分图
1.3.2缺点¶
复杂度较高、不能处理负环图
1.4算法原理¶
我们定义一个三维数组\(f[k][u][v]\)表示的是允许经过\([1,k]\)的点的\(u\)到\(v\)的最小距离,换句话说从\(1\)到\(k\)这些点可以作为\(u\)到\(v\)的 中间节点 ,当然没也可以不经过,很显然我们如果要求解\(u\)到\(v\)的最小距离那么就是\(f[n][u][v]\)(假设当前的图中有n个点的话),那么我们考虑怎么来维护这个关系呢,首先初始化来说,\(f[0][u][v]\)先初始化为INF,如果有边连接的话,那么我们取一个min就好,还有就是如果u和v相等的话应该初始化为0,那么我们就能推出这个状态是如何转移的:
我们对经过k点和不经过k点去一个min,那么我们的状态转移方程就构造好啦,下面给出代码
void Floyd(){
for(int k = 1;k <= n; ++k)
for(int i = 1;i <= n; ++i)
for(int j = 1;j <= n; ++j)
f[k][i][j] = min(f[k-1][i][j],f[k-1][i][k]+f[k-1][k][j]);
}
我们发现我们这个第一维的k其实最多能用到当前这一层以及上一层的状态,那么我们可以通过 滚动数组 优化将其去掉,那么新的代码即为:
void Floyd(){
for(int k = 1;k <= n; ++k)
for(int i = 1;i <= n; ++i)
for(int j = 1;j <= n; ++j)
f[i][j] = min(f[i][j],f[i][k]+f[k][j]);
}
关于第一维对结果无影响的证明 :
我们注意到如果放在一个给定第一维
k二维数组中,f[x][k]与f[k][y]在某一行和某一列。而f[x][y]则是该行和该列的交叉点上的元素。现在我们需要证明将
f[k][x][y]直接在原地更改也不会更改它的结果:我们注意到f[k][x][y]的涵义是第一维为k-1这一行和这一列的所有元素的最小值,包含了f[k-1][x][y],那么我在原地进行更改也不会改变最小值的值,因为如果将该三维矩阵压缩为二维,则所求结果f[x][y]一开始即为原f[k-1][x][y]的值,最后依然会成为该行和该列的最小值。故可以压缩。
模板题:多源最短路
代码实现¶
#include<bits/stdc++.h>
using namespace std;
const int N = 2e2+10;
const int INF = 0x3f3f3f3f;
int n,m,k;
int f[N][N];
void Floyd(){
for(int k = 1;k <= n; ++k)
for(int i = 1;i <= n; ++i)
for(int j = 1;j <= n; ++j)
f[i][j] = min(f[i][j],f[i][k]+f[k][j]);
}
int main()
{
cin>>n>>m>>k;
int u,v,w;
for(int i = 1;i <= n; ++i)
for(int j = 1;j <= n; ++j)
f[i][j] = i==j?0:INF;
for(int i = 1;i <= m; ++i){
cin>>u>>v>>w;
f[u][v] = min(f[u][v],w);
}
Floyd();
while(k--){
cin>>u>>v;
if(f[u][v] > INF / 2) cout<<"impossible"<<endl;
else cout<<f[u][v]<<endl;
}
return 0;
}
二、Bellman-Ford 算法¶
2.1简介¶
\(Bellman-Ford\) 算法是一种基于松弛(\(relax\))操作的最短路算法,可以求出有负权的图的最短路,并可以对最短路不存在的情况进行判断。当然你可能没听过这个算法,但是应该听过另一个算法\(SPFA\) 算法,\(SPFA\)算法其实就是加入了队列优化的\(Bellman-Ford\)
2.2复杂度¶
2.2.1时间复杂度¶
\(O(NM)\)
2.2.2空间复杂度¶
邻接矩阵:\(O(N^2)\)
邻接表:\(O(M)\)
2.3优缺点¶
2.3.1优点¶
能够处理负权图、能处理边数限制的最短路
2.3.2缺点¶
复杂度不太理想,很容易被卡
2.4算法原理¶
2.4.1松弛操作¶
在介绍该算法前,先来介绍一下 松弛操作 ,对于一个边\((u,v)\),松弛操作对应下面的式子:\(dis[v]=min(dis[v],dis[u]+w(u,v))\)。也就是我们将源点到v点的距离更新的一个操作
也就是开始可能源点\(S\)到\(v\)的路径为\(S->v\),如果说经过\(u\)点后再到\(v\)的权值比直接到v小那么我们就更新一下路径最小值,这就是松弛操作
2.4.2 具体流程¶
Bellman算法要做的事就是对于图中所有的边,我们都进行一次松弛操作,那么完成这整个操作的复杂度大概在\(O(M)\),然后我们就一直循环的进行这个操作, 直到我们不能进行松弛操作 为止,就说明我们的单源最短路以及全部求完,那么我们需要多少次这样的完整操作呢, 在最短路存在的情况下 ,由于一次松弛操作会使最短路的边数至少+1 ,而最短路的边数最多为\(N-1\) ,因此整个算法最多执行\(N-1\)轮松弛操作。故总时间复杂度为\(O (NM)\)。
2.4.3 负环问题¶
上面提到了我们在求最短路存在的情况最多执行\(N-1\)轮松弛操作,如果数据中 出现了负环 ,那么我们在 第N轮 操作的时候也会更新
注意一点 :
以\(S\)点为源点跑 Bellman-Ford 算法时,如果没有给出存在负环的结果,只能说明从\(S\)点出发不能抵达一个负环,而不能说明图上不存在负环。 因为这个图可能是不连通的 ,那么对于不连通的图我们应该建一个虚点或者称之为 超级源点 ,让这个点连向每一个其他的点并且权值为0,然后再来跑\(bellman\_ford\)
2.4.4 算法图解¶
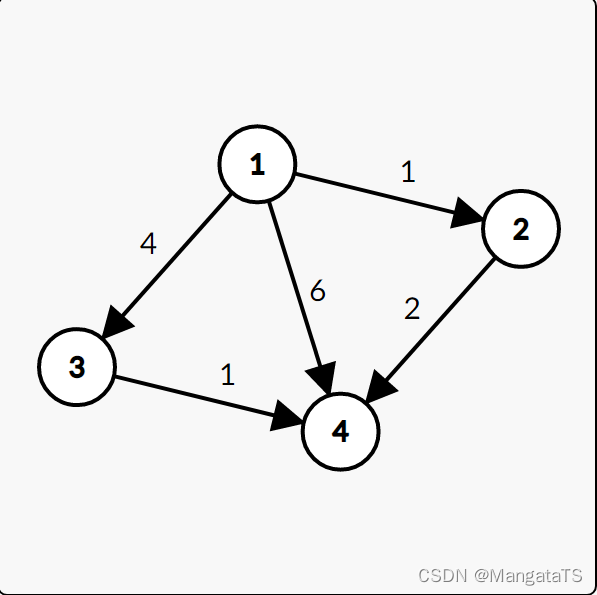
| 第x轮松弛操作 | 本轮松弛操作 |
|---|---|
| 1 | dis[2] =1,dis[3]=4,dis[4]=6 |
| 2 | dis[4]=3 |
| 3 | 无操作 |
模板题:https://ac.nowcoder.com/acm/contest/27274/E
2.5代码实现¶
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstdio>
#include<vector>
const int INF = 0x3f3f3f3f;
const int N = 10000+10;
using namespace std;
struct Node{
int u,v,w;
};
vector<Node> E;
int n,m,s,t;
int dis[N];
void bellman_ford(int s){
for(int i = 1;i <= n; ++i) dis[i] = INF;
dis[s] = 0;
for(int i = 1;i <= n; ++i)
for(int j = 0;j < 2 * m; ++j) {
int u = E[j].u,v = E[j].v,w = E[j].w;
if(dis[v] > dis[u] + w)
dis[v] = dis[u] + w;
}
}
int main()
{
cin>>n>>m>>s>>t;
int u,v,w;
for(int i = 1;i <= m; ++i) {
cin>>u>>v>>w;
E.push_back({u,v,w});
E.push_back({v,u,w});
}
bellman_ford(s);
if(dis[t] >= INF / 2) cout<<"-1"<<endl;
else cout<<dis[t]<<endl;
}
2.6判负环实现¶
如果我们发现第\(N\)轮操作也更新了那么说明存在负权回路
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define INF 0x3f3f3f3f
const int N = 2e6+10;
int n,m,q,k;
struct Edge{
int u,v,w;
}E[N];
int dis[N];
bool bellman_ford(){
for(int i = 1;i <= n; ++i)
for(int j = 0;j < m; ++j) {
int u = E[j].u,v = E[j].v,w=E[j].w;
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
if(i == n)
return true;
}
}
return false;
}
int main()
{
cin>>n>>m;
for(int i = 0;i < m; ++i) {
int u,v,w;
cin>>u>>v>>w;
E[i]={u,v,w};
}
bool k = bellman_ford();
if(k) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}
三、SPFA¶
3.1简介¶
关于SPFA,它死了
3.2复杂度¶
3.2.1时间复杂度¶
理想复杂度为\(O(KM)\),这里的\(K\)可以看作一个常数
最坏为\(O(NM)\)但是一般情况下是跑不到这么多(除非出题人卡SPFA)
3.2.2空间复杂度¶
邻接表:\(O(M)\)
邻接矩阵:\(O(N^2)\)
3.3优缺点¶
3.3.1优点¶
好写、效率挺快(一般来说即不被卡的话),能处理几乎所有类型的图
3.3.2缺点¶
容易被网格菊花图卡成傻b
3.4算法原理¶
3.4.1思想¶
其实\(SPFA\)算法就是\(bllman\_ford\)算法加上了 队列优化 ,我们在上面的\(bellman\_ford\)算法能知道我们实际上是将每一个边都松弛了\(N-1\)次,实际上我们没必要松弛每一个点,因为有些点实际上是不用松弛太多或者说不用松弛的,那么我们希望去掉一些 无用的松弛操作 ,这个时候我们用队列来维护 哪些点可能会需要松弛操作 ,这样就能只访问 必要的 边了。同样的由于SPFA是队列优化的\(bellman\_ford\)那么同样能处理 负权回路 的图
tips:
虽然在大多数情况下 \(SPFA\) 跑得很快,但其最坏情况下的时间复杂度为\(O(NM)\),将其卡到这个复杂度也是不难的,所以考试时要谨慎使用(在没有负权边时最好使用 \(Dijkstra\) 算法,在有负权边且题目中的图没有特殊性质时,若 \(SPFA\) 是标算的一部分,题目不应当给出 \(Bellman-Ford\) 算法无法通过的数据范围)。
3.4.2流程¶
用dis数组记录源点到有向图上任意一点距离,其中源点到自身距离为0,到其他点距离为INF。将源点入队,并重复以下步骤:
- 队首t出队, 并将t标记为没有访问过 ,方便下次入队松弛
- 遍历所有以队首为起点的有向边\((t,j)\),若\(dis[j] > dis[t] + w(t,j)\),则更新\(dis[j]\)
- 如果点\(j\)不在队列中 ,则\(j\)入队, 并将j标记为访问过
- 若队列为空 ,跳出循环;否则执行第一步
我们会发现SPFA的这个过程就和BFS是类似的,如果图是 随机生成 的,时间复杂度为 O(KM) (K可以认为是个常数,m为边数,n为点数)但是实际上SPFA的算法复杂度是 O(NM) ,可以构造出卡SPFA的数据,让SPFA超时。所以使用\(SPFA\)前一定要三思
3.4.3算法图解¶

| 不在队列的元素 | 在队列的元素 | 当前松弛操作 |
|---|---|---|
| \(\{2,3,4 \}\) | \(\{ 1\}\) | \(dis[3]=4,dis[2]=2,dis[4]=6\) |
| \(\{1 \}\) | \(\{2,3,4 \}\) | dis[4]=3 |
| \(\{1,2 \}\) | \(\{3,4 \}\) | 无操作 |
| \(\{1,2,3 \}\) | \(\{4 \}\) | 无操作 |
| \(\{1,2,3,4 \}\) | \(\{\varnothing \}\) | 无操作 |
3.5bellman-ford的其他优化¶
除了队列优化(SPFA)之外,Bellman-Ford 还有其他形式的优化,这些优化在部分图上效果明显,但在某些特殊图上,最坏复杂度可能达到指数级。
- 堆优化:将队列换成堆,与 Dijkstra 的区别是允许一个点多次入队。 在有负权边的图可能被卡成指数级复杂度 。
- 栈优化:将队列换成栈(即将原来的 BFS 过程变成 DFS), 在寻找负环时可能具有更高效率,但最坏时间复杂度仍然为指数级 。
- \(LLL\) 优化:将普通队列换成双端队列, 每次将入队结点距离和队内距离平均值比较,如果更大则插入至队尾,否则插入队首 。
- \(SLF\) 优化:将普通队列换成双端队列, 每次将入队结点距离和队首比较,如果更大则插入至队尾,否则插入队首 。
- \(D´Esopo-Pape\) 算法:将普通队列换成双端队列, 如果一个节点之前没有入队,则将其插入队尾,否则插入队首 。
既然有了优化,那么就会有相应的卡的方法,具体请看这一篇回答:https://www.zhihu.com/question/292283275/answer/484871888
模板题:https://ac.nowcoder.com/acm/contest/27274/E
3.6 SPFA最短路代码实现¶
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
const int INF = 0x3f3f3f3f;
const int N = 10000+10;
using namespace std;
struct Node{
int v,w;
};
vector<Node> E[N];
int n,m,s,t;
int dis[N];
bool vis[N];
void SPFA(int s){
for(int i = 1;i <= n; ++i)
vis[i] = false,dis[i] = INF;
queue<int> que;
que.push(s);
dis[s] = 0,vis[s] = true;
while(!que.empty()){
int t = que.front();
que.pop();
vis[t] = false;
for(int i = 0,l = E[t].size();i < l; ++i) {
int j = E[t][i].v;
int k = E[t][i].w;
if(dis[j] > dis[t] + k){
dis[j] = dis[t] + k;
if(!vis[j]){
vis[j] = true;
que.push(j);
}
}
}
}
}
int main()
{
cin>>n>>m>>s>>t;
int u,v,w;
for(int i = 1;i <= m; ++i) {
cin>>u>>v>>w;
E[u].push_back({v,w});
E[v].push_back({u,w});
}
SPFA(s);
if(dis[t] >= INF / 2) cout<<"-1"<<endl;
else cout<<dis[t]<<endl;
}
3.7 SPFA判负环实现¶
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<queue>
#include<vector>
using namespace std;
#define PII pair<int,int>
const int N = 2e6+10;
int n,m,q;
vector<PII> E[N];
int dis[N],cnt[N];
bool vis[N];
void spfa(){
queue<int> que;
for(int i = 1;i <= n; ++i) que.push(i),vis[i] = true;
while(!que.empty()){
int t = que.front();
que.pop();
vis[t] = false;//表明t这个点已经离开这个队列了
for(int i = 0,l = E[t].size();i < l; ++i) {
int j = E[t][i].first,k = E[t][i].second;
if(dis[j] > dis[t] + k) {
dis[j] = dis[t] + k;
cnt[j] = cnt[t] + 1;
if(cnt[j] >= n) {//找到负权边
cout<<"Yes"<<endl;
return;
}
if(!vis[j])//将j这个点重新加入队列
que.push(j),vis[j] = true;
}
}
}
cout<<"No"<<endl;
}
int main()
{
cin>>n>>m;
int u,v,w;
for(int i = 0;i < m; ++i) {
cin>>u>>v>>w;
E[u].push_back({v,w});
}
spfa();
return 0;
}
3.8 SPFA判断正环¶
关于\(SPFA\)判断正环的可以参考这一题:https://blog.csdn.net/m0_46201544/article/details/123011318
四、Dijkstra算法¶
4.1简介¶
\(dijkstra\)是一种单源最短路径算法,时间复杂度上限为 \(O(n^2)\) (朴素),在实际应用中较为稳定 ; 加上堆优化之后更是具有\(O((n+m)\log_{2}n)\) 的时间复杂度,在稠密图中有不俗的表现.
\(Dijkstra(/ˈdikstrɑ/或/ˈdɛikstrɑ/)\)算法由荷兰计算机科学家 \(E. W. Dijkstra\) 于 \(1956\) 年发现,\(1959\) 年公开发表。是一种求解 非负权图 上单源最短路径的算法。
贪心思想
4.2复杂度¶
4.2.1空间复杂度¶
4.2.1.1朴素Dijkstra¶
\(O(N^2)\)
4.2.1.2链式前向星优化+Dijkstra¶
\(O(M)\)
4.2.2时间复杂度¶
4.2.2.1 朴素Dijkstra¶
\(O(N^2)\)
4.2.2.2 链式前向星+堆优化的Dijkstra¶
\(O((n+m)\log_{2}n)\)
4.3优缺点¶
4.3.1 优点¶
朴素\(Dijkstra\)和堆优化的\(Dijkstra\)基本上能解决所有的正权图最短路问题, 时间复杂度不会受到限制
4.3.2 缺点¶
不能处理负权图,如果需要处理负权图请移步\(SPFA\)
但是在某些 特定的 含有负边的图DJ也是对的例如:
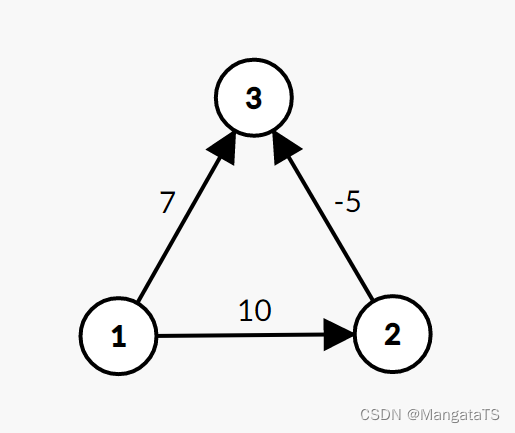
但是我们稍加变换,迪杰斯特拉就不能处理了:
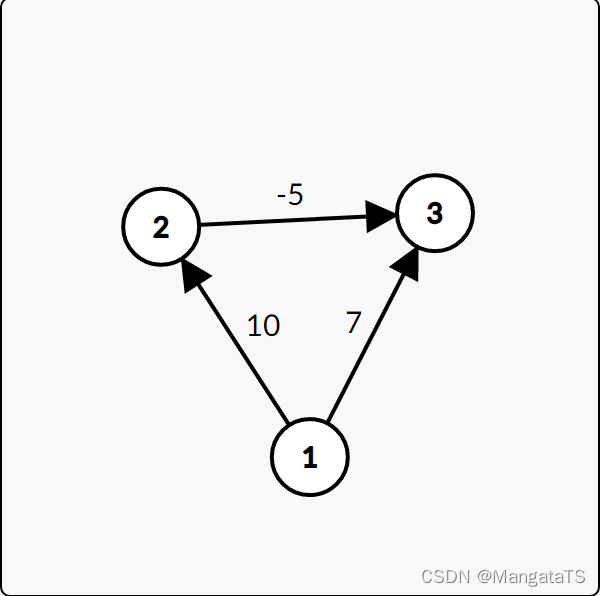
4.4 算法原理¶
4.4.1思想¶
\(Dijkstra\)的核心思想其实就是贪心思想,每次寻找一个 临近点的dis值最小 的点,然后我们再来对该点进行松弛操作
4.4.2 流程¶
将结点分成两个集合:已确定最短路长度的点集(记为\(S\)集合)的和未确定最短路长度的点集(记为\(T\)集合)。一开始所有的点都属于\(T\)集合。
- 1.初始化 \(dis[start] = 0\), 其余节点的 \(dis\) 值为无穷大
- 2.从\(T\)集合中选取一个从源点到该点的最短路值最小的点\(x\),然后放入\(S\)集合中(我们可以通过 vis数组标记 来实现集合划分)
- 3.遍历 \(x\) 的所有出边 \((x,y,z)\), 若 \(dis[y] > dis[x] + z\), 则令 \(dis[y] = dis[x] + z\)
- 4.重复 2,3 两步,直到所有点都加入集合\(S\) .
- 时间复杂度为 \(O(n^2)\)
4.4.3 算法图解¶
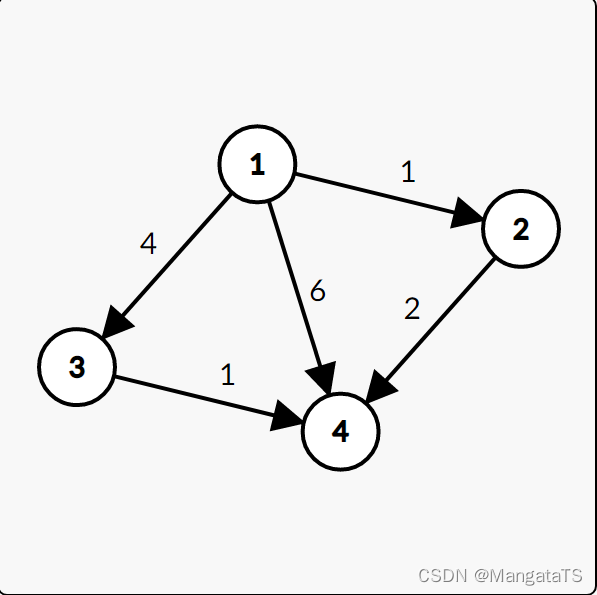
| T集合元素 | S集合元素 | 当前松弛操作 |
|---|---|---|
| \(\{2,3,4\}\) | \(\{1 \}\) | dis[1] = 0,dis[2]=1,dis[3]=4,dis[4]=6 |
| \(\{3,4 \}\) | \(\{1,2\}\) | dis[4] = 3 |
| \(\{ 3\}\) | \(\{1,2,4\}\) | 无 |
| \(\varnothing\) | \(\{1,2,3,4\}\) | 无 |
那么最终我们的dis值就变成了:
\(dis[1] = 0 \\ dis[2] = 1 \\ dis[3] = 4 \\ dis[4] = 3\)
4.5 优化¶
我们发现,对于 寻找\(dis\)值最小 的点的操作,我们通过 不同的方式维护 的话那么算法的整体复杂度就会不同
- 暴力:不使用任何数据结构进行维护,每次 2 操作执行完毕后,直接在\(T\)集合中暴力寻找最短路长度最小的结点。3操作总时间复杂度为\(O(M)\),2操作总时间复杂度为\(O(N^2)\),全过程的时间复杂度为\(O(N^2+M)=O(N^2)\)。
- 二叉堆:每成功松弛一条边\((u,v)\),就将\(v\)插入二叉堆中(如果\(v\)已经在二叉堆中,直接修改相应元素的权值即可),2操作直接取堆顶结点即可。共计\(O(M)\)次二叉堆上的插入(修改)操作,\(O(N)\)次删除堆顶操作,而插入(修改)和删除的时间复杂度均为\(O(log_2N)\),时间复杂度为\(O((N+M)\times log_2N) = O(mlog_2m)\)。
- 优先队列:和二叉堆类似,但使用优先队列时,如果同一个点的最短路被更新多次,因为先前更新时插入的元素不能被删除,也不能被修改,只能留在优先队列中,故优先队列内的元素个数是\(O(M)\)的,时间复杂度为 \(O(Mlog_2M)\)
- Fibonacci 堆:和前面二者类似,但 Fibonacci 堆插入的时间复杂度为\(O(1)\),故时间复杂度为\(O(Nlog_2N+M)=O(Nlog_2N)\),时间复杂度最优。但因为 Fibonacci 堆较二叉堆 不易实现,效率优势也不够大 ,算法竞赛中较少使用。
注意的是:在 稠密图 中通过暴力方式维护效率更好,\(O(N^2)\),在 稀疏图 中通过堆优化的方式维护效率更高,\(O((n+m)\log_{2}n)\)
4.6 正确性证明(引自算法导论)¶
\(dijkstra\) 为什么是正确的呢? ,当我们存储的所有的边都是正权边时,整个图的最小值不可能再被其他节点更新,所以我们在T集合中寻找dis最小值其实就是再选择全局最小值,也就是贪心的思想
下面用数学归纳法证明,在 所有边权值非负 的前提下,Dijkstra 算法的正确性。
简单来说,我们要证明的,就是在执行 1 操作时,取出的结点\(u\)最短路均已经被确定,即满足\(D(u)=dis(u)\) 。
-
初始的时候\(S=\varnothing\) ,假设成立,接下来使用反证法。
-
设\(u\)点为算法中第一个在加入\(S\)集合时不满足\(D(u)=dis(u)\)的点。因为\(s\)点一定满足\(D(u)=dis(u)=0\),且它一定是第一个加入\(S\)集合的点,因此将\(u\)加入\(S\)集合前\(S != \varnothing\),如果不存在\(s\)到\(u\)的路径,则\(D(u)=dis(u)=+∞\) ,与假设矛盾。
-
于是一定存在路径\(s->x->y->u\),其中y为\(s->u\)路径上第一个属于\(T\)集合的点,而\(x\)为\(y\)的前驱节点(显然x∈S)。需要注意的是,可能存在\(s=x\)或者\(y=u\)的情况,即\(s->x\)或者\(y->u\)是一个不存在的路径
-
因为在\(u\)结点之前加入的结点都满足\(D(u)=dis(u)\),所以在\(x\)点加入到\(S\)集合时,有\(D(u)=dis(u)\),此时边\((x,y)\)会被松弛,从而可以证明,将\(u\)加入到\(S\)时,一定有\(D(y)=dis(y)\)。
- 下面证明\(D(u)=dis(u)\)成立。在路径\(s->x->y->u\)中,因为图上所有边边权非负,因此\(D(y)<= D(u)\)。从而\(dis(y)<=D(y)<=D(u)<=dis(u)\)。但是因为\(u\)结点在2 过程中被取出\(T\)集合时,\(y\)结点还没有被取出\(T\)集合,因此此时有\(dis(u)<=dis(y)\),从而得到\(dis(y)=D(y)=D(u)=dis(u)\),这与\(D(u)!=dis(u)\)的假设矛盾,故假设不成立。
- 因此我们证明了,2 操作每次取出的点,其最短路均已经被确定。命题得证。
4.7 代码实现¶
模板题:https://ac.nowcoder.com/acm/contest/27274/E
4.7.1 朴素Dijkstra(稠密图)¶
#include<cstdio>
#include<algorithm>
#include<vector>
#include<iostream>
#include<cstring>
using namespace std;
#define INF 0x3f3f3f3f
const int N = 1e3+10;
int f[N][N],n,m,dis[N];
bool vis[N];
void DJ(int s){
for(int i = 1;i <= n; ++i) dis[i] = INF,vis[i] = false;
dis[s] = 0;
for(int i = 1;i <= n; ++i) {
int t = -1;
for(int j = 1;j <= n; ++j)
if(!vis[j] && (t == -1 || dis[j] < dis[t])) t = j;
if(t == -1) return;
vis[t] = true;
for(int j = 1;j <= n; ++j)
if(dis[j] > dis[t] + f[t][j])
dis[j] = dis[t] + f[t][j];
}
}
int main()
{
int s,t;
cin>>n>>m>>s>>t;
int u,v,w;
memset(f,0x3f,sizeof f);
for(int i = 1;i <= m; ++i){
cin>>u>>v>>w;
f[v][u] = f[u][v] = min(f[u][v],w);
}
DJ(s);
if(dis[t] == INF) cout<<"-1"<<endl;
else cout<<dis[t]<<endl;
return 0;
}
4.7.2 优先队列优化Dijkstra(稀疏图)¶
#include<cstdio>
#include<algorithm>
#include<vector>
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
#define endl "\n"
#define PII pair<int,int>
#define INF 0x3f3f3f3f
const int N = 2e6+10;
int dis[N],n,m;
bool vis[N];
vector<PII> E[N];
void DJ(int s){
for(int i = 1;i <= n; ++i) dis[i] = INF,vis[i] = false;
priority_queue<PII,vector<PII>,greater<PII> > que;
que.push({0,s});
dis[s] = 0;
while(!que.empty()){
int t = que.top().second;
que.pop();
if(vis[t]) continue;
vis[t] = true;
for(int i = 0,l = E[t].size();i < l; ++i) {
int j = E[t][i].first,w = E[t][i].second;
if(dis[j] > dis[t] + w){
dis[j] = dis[t] + w,que.push({dis[j],j});
}
}
}
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int s,t;
cin>>n>>m>>s>>t;
int u,v,w;
for(int i = 1;i <= m; ++i){
cin>>u>>v>>w;
E[u].push_back({v,w});
E[v].push_back({u,w});
}
DJ(s);
if(dis[t] == INF) cout<<"-1"<<endl;
else cout<<dis[t]<<endl;
return 0;
}
4.7.3 链式前向星+优先队列优化Dijkstra¶
#include<cstdio>
#include<cstring>
#include<queue>//
using namespace std;
const int N=2e5+5;//数据范围
struct edge{//存储边
int u,v,w,next;//u为起点,v为终点,w为权值,next为前继
};
edge e[N];
int head[N],dis[N],n,m,s,cnt;//head为链中最上面的,dis表示当前答案,n为点数,m为边数,s为起点,cnt记录当前边的数量
bool vis[N];//vis表示这个点有没有走过
struct node{
int w,to;//w表示累加的权值,to表示到的地方
bool operator <(const node &x)const{//重载“<”号
return w>x.w;
}
};
priority_queue<node>q;//优先队列(堆优化)
void add(int u,int v,int w){
++cnt;//增加边的数量
e[cnt].u=u;//存起点
e[cnt].v=v;//存终点
e[cnt].w=w;//存权值
e[cnt].next=head[u];//存前继
head[u]=cnt;//更新链最上面的序号
}//链式前向星(加边)
void Dijkstra(){
memset(dis,0x3f3f3f3f,sizeof(dis));//初始化,为dis数组附一个极大值,方便后面的计算
dis[s]=0;//起点到自己距离为0
q.push(node{0,s});//压入队列
while(!q.empty()){//队列不为空
node x=q.top();//取出队列第一个元素
q.pop();//弹出
int u=x.to;//求出起点
if(vis[u]) continue;//已去过就不去了
vis[u]=true;//标记已去过
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;//枚举终点
if(dis[v]>dis[u]+e[i].w){//若中转后更优,就转
dis[v]=dis[u]+e[i].w;//更新
q.push(node{dis[v],v});//压入队列
}
}
}
}
int main(){
int u,v,w = 1;
s = 1;
scanf("%d%d",&n,&m);//输入
for(int i=1;i<=m;++i){
scanf("%d%d",&u,&v);
add(u,v,w);
add(v,u,w);
}
Dijkstra();//DJ
printf("%d\n",dis[n]);//输出1-n的最短路
return 0;
}
4.8 路径打印问题¶
我们可以定义一个\(pre\)数组,然后\(pre[i]\)记录的是上一个位置是哪一个节点,当然初始的时候我们全部初始化为\(-1\),然后每次松弛操作的时候就更新一下上一个节点的位置,你有没有发现这就是链式前向星,然后最后打印的时候要么递归打印,那么手动写栈打印,这个方法不只是适用于Dijkstra,而且也适用于其他最短路算法,如\(SPFA\)、\(bellman\_ford\)、\(Floyd\)等等
那么简单描述一下打印函数
void print(int t){
for(int i = t;~i;i=pre[i]){
cout<<i;
if(i != s) cout<<" -> ";
}
}
4.9 路径统计问题¶
其实我们在 松弛操作 的时候就能记录or更新从源点到当前点的路径条数,模板题可以参见下面的:最短路计数
五、Johnson 全源最短路¶
待补充