哈希表|散列表¶
一、 基本概念¶
哈希表（ \(Hash Table\) ）也称为散列表，是根据关键码值( \(Key、Value\) )而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做 散列函数 ，存放记录的数组叫做 散列表 。
其实可以简单理解为一张表里面存储了一些我们需要使用的元素，这些元素都有关键字，我们将关键字输入散列函数处理，然后给我们映射到一个地址，我们访问这个地址就能得到我们想要的元素
显然散列函数在帮我们映射关键字地址的时候难免会将不同的关键字映射到同一个地址，这种情况就是 冲突，或称哈希冲突 ，一般来说这样的冲突是无可避免的，所以在发生冲突前我们尽量设计好 散列函数 ，当然在发生冲突后我们也需要指定一系列的操作用于处理冲突，下面会一一道来。
通过上面的介绍，我们会发现哈希表的出现就是结合了数组和链表的优点的，数组的特点是寻址容易，插入和删除难，而链表的特点是寻址困难，但是插入和删除容易，而哈希表很显然我们会发现插入很容易，删除也很容易（理想情况下）
二、 哈希函数|散列函数¶
在构造散列函数需要注意几点： - 散列函数的定义域一定要包含全部存储的关键字，值域的范围依赖于散列表的大小 - 散列函数计算出来的地址应尽量等概率均匀分布在整个地址空间，从而减少冲突 - 散列函数的设计应当尽量简单，能够在较短时间内计算出任意关键字对应的地址
下面则是常用的散列函数：
2.1 直接定址法¶
散列函数为一个线性函数，我们通过将关键字传入计算出相应的散列地址：
其中 \(a\) 和 \(b\) 为常数，因为是线性函数，即 一对一的模式，所以不会产生哈希冲突，他适合关键字分布基本连续的情况，否则会造成存储空间的浪费
2.2 保留余数法¶
假设散列表长为 \(m\) ,取一个不大于 \(m\) 的最大质数 \(p\) 哈希函数为：
2.3 数字分析法¶
设关键字是 \(r\) 进制数（如十进制数），而 \(r\) 个数码在各位上出现的频率不一定相同 ，可能在某些位上分布均匀一些，每种数码出现的机会均等；而在某些位上分布不均匀，只有某几种数码经常出现，此时应选取数码分布较为均匀的若干位作为散列地址。 这种方法适合于己知的关键字集合，若更换了关键字， 则需要重新构造新的散列函数
2.4 平方取中法¶
将关键字的平方值的中间几位作为散列值，具体取多少位根据实际情况而定（感觉很鸡肋……）
2.5 折叠法¶
将关键字分割成位数相同的几部分（最后一部分可以不同），然后再将这几部分累加起来作为哈希地址
例如一个电话 \(18784878052\) 我们将其分割成每一部分三位数字，从前往后分割，就得到了这几个数：\(\{187,848,780,52 \}\) 然后我们再将其累加起来得到：
这样就是一个折叠发的映射处理了~
2.6 随机数法¶
这……就很顾名思义了，通过伪随机数作为关键字的映射地址（这个也很鸡肋，知道就行了）
三、冲突处理¶
在某些哈希函数的处理下，冲突是无法避免的，那么解决哈希冲突大概有以下的方法：
3.1 开放定址法¶
当哈希冲突发生的时候，通过往后探测，找到一个空位，显然往后探测的方法不同，也就划分了不同的方式，简单理解为，你在学校准备上厕所，你一眼相中了第二个坑位，当你过去的时候你发现里面有人了（这就是冲突），然后你得去找下一个没有人的坑位（解决冲突），那么你是直接到下一个坑位查看有没有人呢，还是说直接跳三个坑位再看（解决冲突的方法）
一般的开放地址法的递推公式如下：
其中， \(H(key)\) 为散列函数， \(i=0,1,2……,k(k<=m-1)\) ， \(m\) 表示散列表的长度， \(d_i\) 表示每次探测的增量
那么下面就来正式介绍一下这些处理冲突的方法吧。
3.1.1 线性探测¶
线性探测发就是依次往后探测，每次探测的增量为 \(1\) ,即如果当前映射地址发生冲突了，那么我们就往下一个单元探测，假设也发生了冲突，那么我们就继续往下一个位置探测，直到找到一个空闲的单元
道理很简单，我们来看看这样做可能造成的后果：这样做可能会让第 \(i\) 个散列地址的 同义词（即不同关键字映射到同一地址的情况） 存入第 \(i+1\) 个散列地址，然后本应该在 \(i+1\) 个位置存储的元素会往后迁移……从而会造成大量的元素在相邻的散列地址上 聚集或是堆积 起来，就会大大的降低查找的效率
3.1.2 平方探测¶
平方探测就是将探测的增量变为 \(d_i = 0^2,1^2,2^2,3^2,4^2……k^2,-k^2\) ，其中 \(k<=\frac{m}{2}\) ，散列表的长度 \(m\) 必须是一个可以表示为 \(4k+3\) 的 素数 ，又称为 二次探测法
优点：可以解决线性探测发引发的关键字堆积问题，但是缺点是不能探测到散列表上的所有单元，但是至少能探测到一半的单元
3.1.3 双散列法¶
双散列法又称为 再散列法 ，即通过两个散列函数进行地址计算，然后再对长度取模，当然第二个散列函数是从一个散列函数表中从前往后抽取的，如果第 \(i\) 个散列函数计算出来的地址仍然冲突，那么就拿 \(i+1\) 个散列函数重新计算，直到不发生冲突为止，具体形式如下：
其中 \(i\) 就为冲突的次数，初始的时候为 \(0\) ， 第二种写法 最多经过 \(m-1\) 次探测就会遍历表中所有的为止回到 \(H_0\)
3.1.4 伪随机序列法¶
显然是将 \(d_i\) 设为一个随机数作为映射地址（感觉……没啥用）
3.2 链地址法 | 拉链法¶
这个方法思路很简单，结合了链表的思想，因为可能会有不同的关键字映射在同一个地址，那么为了避免这种冲突的情况，我们就将所有的 同义词 存放在以这个地址为首地址的链表上面，当我们每次查询的时候通过关键字映射到这个地址，我们就可以直接在这一条链表上面遍历查找
例如假设有一个关键字序列：\(\{19,14,23,01,68,20,84,27,55,11,10,79 \}\) ，然后散列函数是 \(H(key)=key \%13\) 然后我们通过拉链法处理冲突得到如下图所示：
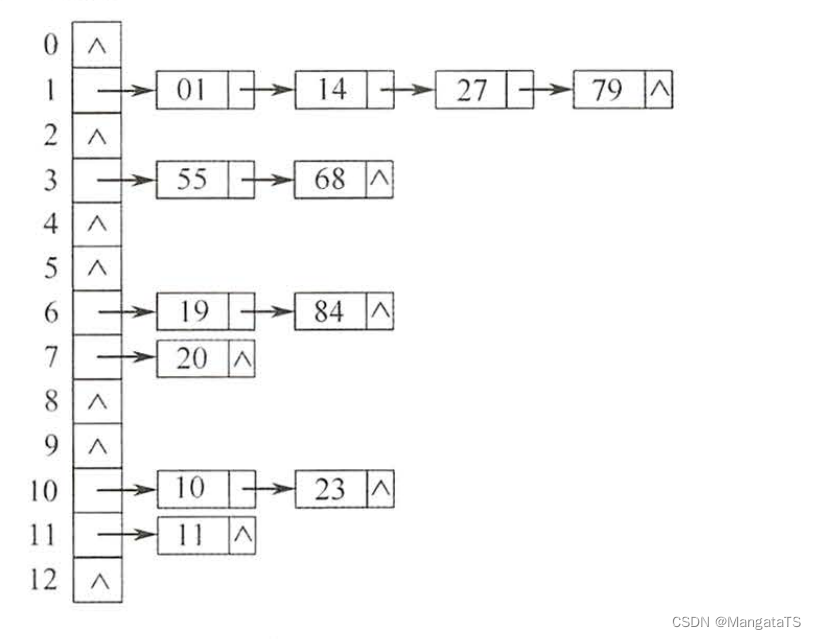
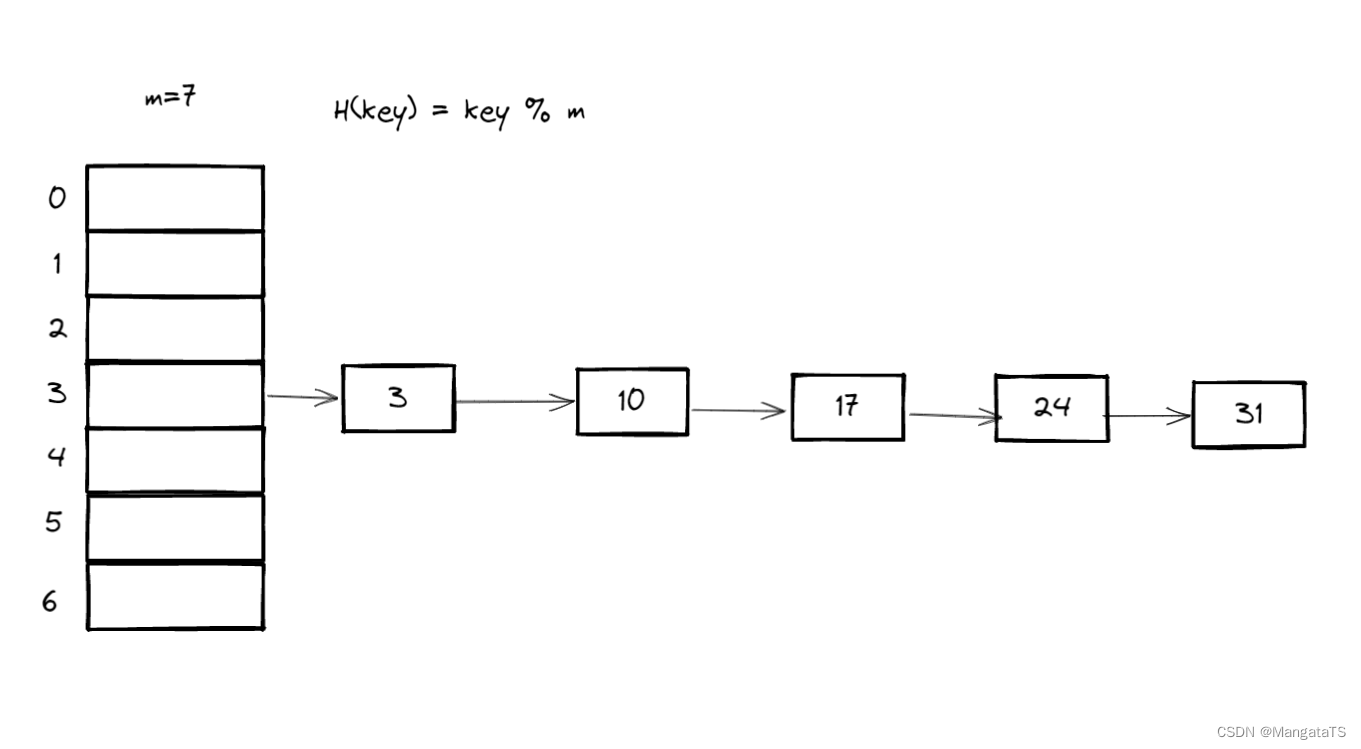
但是链地址法也有一定的问题，假设我们的关键字互相都是同义词，那么我们的哈希表就会变成一个链表，那么效率就直接退化了，例如我们的关键字序列：${3,10,17,24,31} ，哈希表的长度为 \(7\) 那么得到的哈希表如下图所示：
四、 性能分析¶
虽然散列表在关键字与记录的存储位置之间建立了直接映像，但由于 “冲突” 的产生，使得散列表的查找过程仍然是一个给定值和关键字进行比较的过程。 因此，仍需要以 平均查找长度（ASL） 作为衡量散列表的查找效率的度量。
那么对于哈希表的平均查找长度是怎么计算的呢？
首先先假设是查找的元素一定存在，且散列表中插入了 \(n\) 个元素，忽略查找失败的情况：
那么对于失败的平均查找长度的话，假设散列函数是 \(H(key) = key % \m\) 这里的 \(m\) 是散列函数的约束长度，而实际的散列表应当大于这个值，且已经插入了 \(n\) 个元素，那么我们就能得到：
例如，下面的题目：
我们先将散列表画出来：
假如我们查找的元素映射到地址 \(0\) ，我们就需要从 \(0\) 开始比对，直到找到地址 \(8\) ，我们发现后面没关键字了，于是确定了我们查询的关键字不在散列表中，即查找失败，因为我们的散列函数只有 \([0,7]\) 这个区间，于是我们就得到了其失败平均查找长度：\(ASL_{失败} = \frac{9+8+7+6+5+4+3}{7} = 6\)