考研数据结构与算法(八)查找¶
一、基本概念¶
1.1 查找表¶
用于查找的数据集合称为查找表,它由 同一类型 的数据元素(或记 录〉组成,可以是一个数组或链表等数据类型。
查找表中常用的四种操作 - ①查询某个 特定的数据元素 是否在查找表中 - ②检索满足条件的某个特定的数据元素的其他属性 - ③在查找表中 插入 一个数据元素 - ④从查找表中 删除 某个数据元素
只进行查找(检索)操作(即查找表的前两种操作)的表另称为 静态查找表 ,如果需要进行 删除 或者 插入 操作,那么此表另称为 动态查找表
1.2 关键字¶
对于一个数据元素,可能是多个值构成的,每一个值都是一个关键字,如果一个关键字在查找表里可以 唯一的标识 一个记录,那么我们称其为 主关键字 ,若不能唯一标识我们则称其为 次关键字
1.3 查找¶
根据某个给定的值,在查找表寻找满足条件的过程称为查找,查找的结果一般分为两种: - 查找成功 - 查找失败
1.4 平均查找长度¶
在查找过程中,一次查找的长度是指需要 比较的关键字次数 ,而平均查找长度则是所有查找过程中进行关键字的比较次数的平均值,一般来说 这个平均长度是指 平均成功查找长度 因为查找不成功的情况我们一般忽略掉了,但是如果我们不能忽略查找失败的情况,那么某个算法的 平均查找长度=成功平均查找长度 + 失败平均查找长度
1.4.1 成功平均查找长度¶
注意:这个在所有的查找表的题目中都会考到,后面对于每一个表都会进行分析
我们假设 \(n\) 是查找表的长度, \(P_i\) 是查找第 \(i\) 个数据元素的概率(一般认为每一个数据元素查找的概率相等,即 \(P_i = 1/n\)) ,\(C_i\) 是找到第 \(i\) 个数据元素所需要进行的比较次数,则其数学定义为:
1.4.2 失败平均查找长度¶
注意:这个只在二叉排序树or哈希表中可能会考到,后面也会一一解析
对于一个查找表来说,假设对于查找某个不存在的元素的概率为 \(P_i\) ,对每一个不存在的元素查找所需要进行的比较次数为 \(C_i\) ,假设我们有 \(m\) 个不存在的元素,那么我们可以得到其数学定义:
这里其实不够形象,可以不用在意,后面会具体例子具体解析的~
二、静态查找¶
2.1 顺序表(顺序查找)¶
简单理解为,我们将元素存储在一个线性表中,这个线性表可以是数组也可以是链表,反正无论如何我们都是要从头到尾遍历,除非遇到我们需要查找的元素,我们就将元素返回,否则我们就继续往下遍历,最后没找到的话,我们可以返回一个 -1 或者其他非元素集合下标
关于代码的话一般有两种写法,第一种则是王道书上介绍的 “哨兵” 写法,我们将线性表中第 \(0\) 个位置设定为我们想要找的元素(即线性表中的元素是 \([1,n]\) 范围的),然后从线性表的末尾往前查找,即便 \([1,n]\) 范围内没有我们需要的元素,也会在第 \(0\) 个位置停止,此时我们对于函数返回的值做判断只要是 \(0\) 那么就说明没找到
typedef struct{//查找表的数据结构
ElemType *elem; //元素存储空间基址,建表时按实际长度分配,0 号单元留空
int TableLen; //表的长度
}SSTable;
int Search_Seq(SSTable ST , ElemType key) {
ST.elem[0]=key; //“哨兵”
for(i = ST.TableLen; ST.elem[i] != key; --i); //从后往前找
return i; //若表中不存在关键字为 key 的元素,将查找到 i 为 0 时退出 for 循环
}
当然如果说我们想要元素从 \(0\) 这个位置开始存储的话,可以不不使用 “哨兵” ,代码如下
typedef struct{//查找表的数据结构
ElemType *elem; //元素存储空间基址,建表时按实际长度分配
int TableLen; //表的长度
}SSTable;
int Search_Seq(SSTable ST , ElemType key) {
for(i = ST.TableLen - 1; i >= 0; --i); //从后往前找
if(ST.elem[i] == key)
return i; //表中找到关键字 key
return -1;//表中未找到关键字
}
对于这样的一个查找方法,我们来分析一下它的平均查找长度: - 对于查找第 \(i\) 个元素,如果我们逆着查找那么需要比较 \(n-i+1\) 次,顺着看实际上我们就需要比较 \(i\) 次,不管是顺着还是逆着,当我们求平均的时候结果都是一样的,但是显然顺着的方式比较好求一点 - 又由于每一个元素查找的可能都是一样的即 \(\frac{1}{n}\) 于是 \(P_i = \frac{1}{n}\) ,那么对于顺序查找的平均长度就为:
当然上式子若是逆着查找的话应该这么写:
反正结果是一样的啦~
我们 考虑一下查找失败的情况 ,假设查找失败的概率和查找成功的概率一样,那么对于查找失败的情况来说每一次查找的概率是和已经有元素一样即 \(P_i = \frac{1}{2n}\) ,而每次匹配的次数都是 \(n\) 次( 从头到尾匹配完,这里使用的是非哨兵模式 ),那么失败平均匹配长度为:
此时的成功平均匹配长度为:
所以平均匹配长度为:
假设我们的顺序表是一个有序表的话,那么我们进行失败匹配的过程中会减少一点,假设我们走到了一个大于查找的 key 的第一个位置,因为顺序表是一个有序的,那么我们现在就需要停止,那么对于第 \(i\) 个未查找到的元素我们需要比较 \(i+1\) 次,那么对于匹配失败的概率是 \(\frac{1}{2n}\) ,匹配失败的长度为
那么对于失败匹配的平均长度为:
假设对于一个 \(n\) 为 \(10\) 的顺序表而言,如果是乱序,那么其失败查找长度为: \(5\) ,若是有序的话,其失败匹配平均长度为 \(\frac{13}{4}\) ,可以看得出确实有一定提升
注意: - 一般来说,仅讨论 查找成功的平均查找长度 或者是 查找不成功的比较次数 - 上面所用例子以及匹配此时可能和 王道/严蔚敏 书上有所不同,不同点其实就在于比较次数
2.2 有序表(二分查找)¶
这一块着重于介绍二分查找(折半查找)这一算法,能够在有序表中高效的查找我们所需的信息,详细的讲解可以观看下面的博客(内附视频) https://acmer.blog.csdn.net/article/details/118559948
举一个二分查找的例子,假设有如下的序列 \(a\) :
简单绘画一下(下标从 \(1\) 开始)
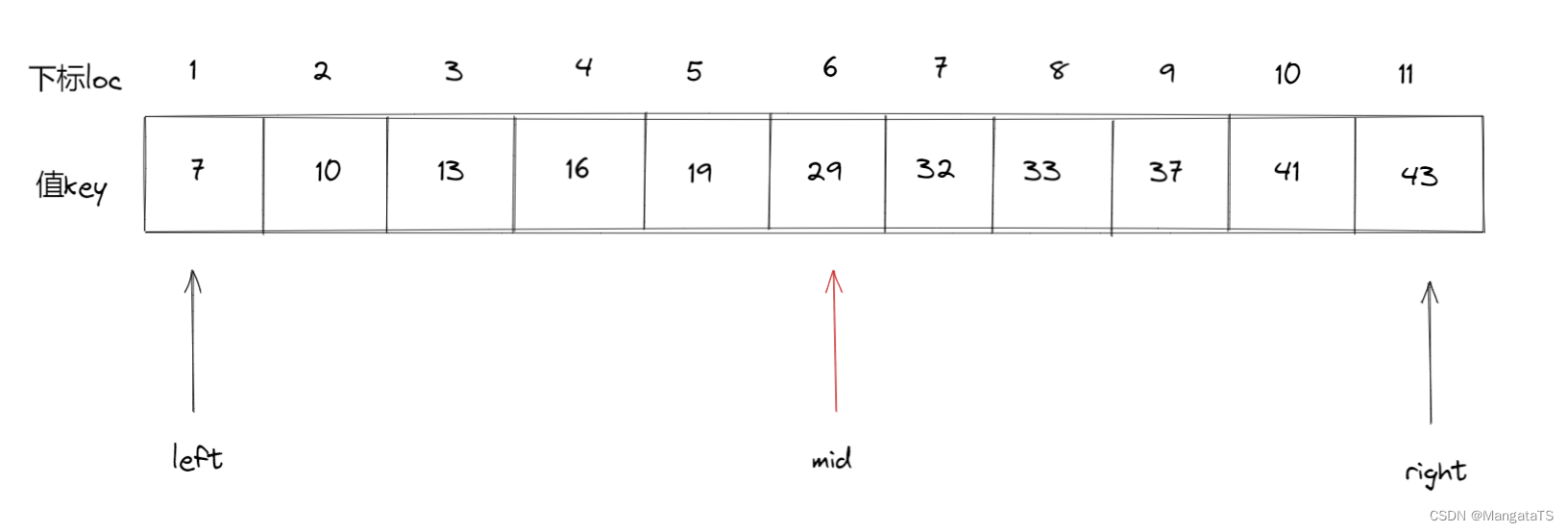
假设我们要查找 \(32\) 这个元素,那么查找过程如下:
- 第一次查找:\(mid = \left \lfloor \frac{\text{left}+\text{right}}{2} \right \rfloor =\left \lfloor \frac{1+11}{2} \right \rfloor = 6\) 于是我们就将 \(a[6]\) 和 \(32\) 进行比较,我们发现 \(a[6] < 32\) 于是我们将 \(left\) 更新,即 \(left = mid + 1 = 7\) ,\(right\) 不变,还是 \(11\)
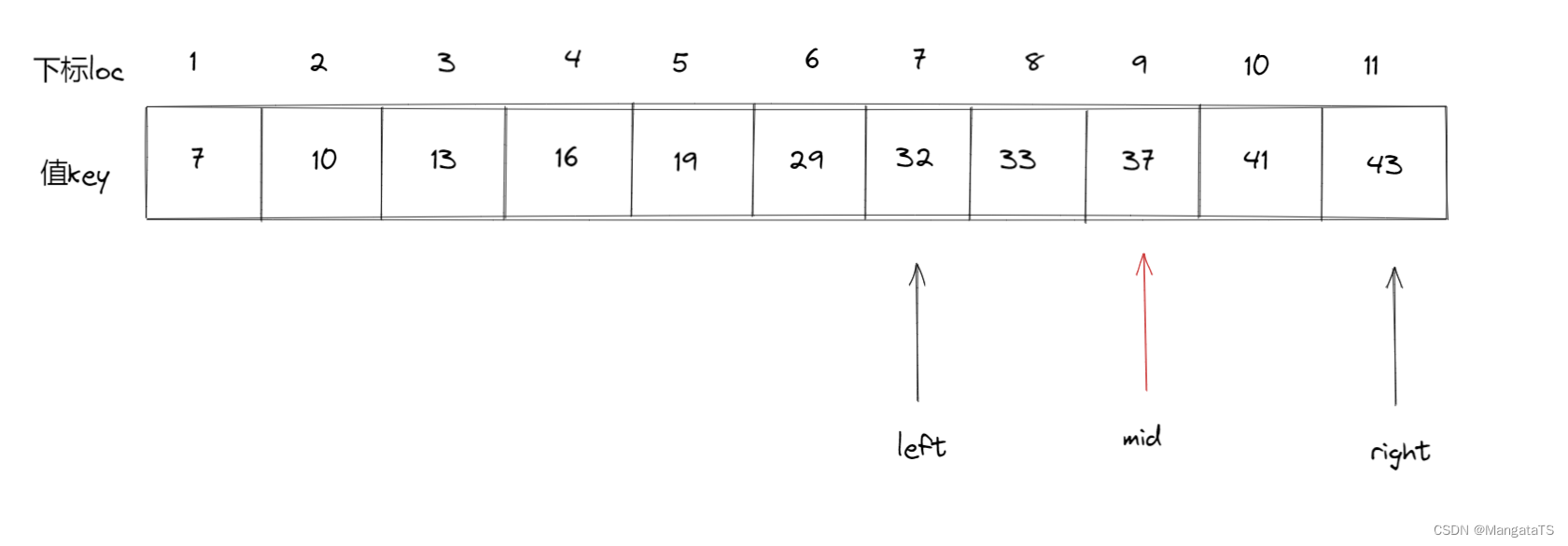
- 第二次查找: \(mid = \left \lfloor \frac{\text{left}+\text{right}}{2} \right \rfloor =\left \lfloor \frac{7+11}{2} \right \rfloor = 9\) 于是我们将 \(a[9]\) 和 \(32\) 进行比较,我们发现 \(a[9] > 32\) 于是我们将 \(right\) 更新,即 \(right = mid - 1 = 8\) , \(left\) 不变,还是 \(7\)
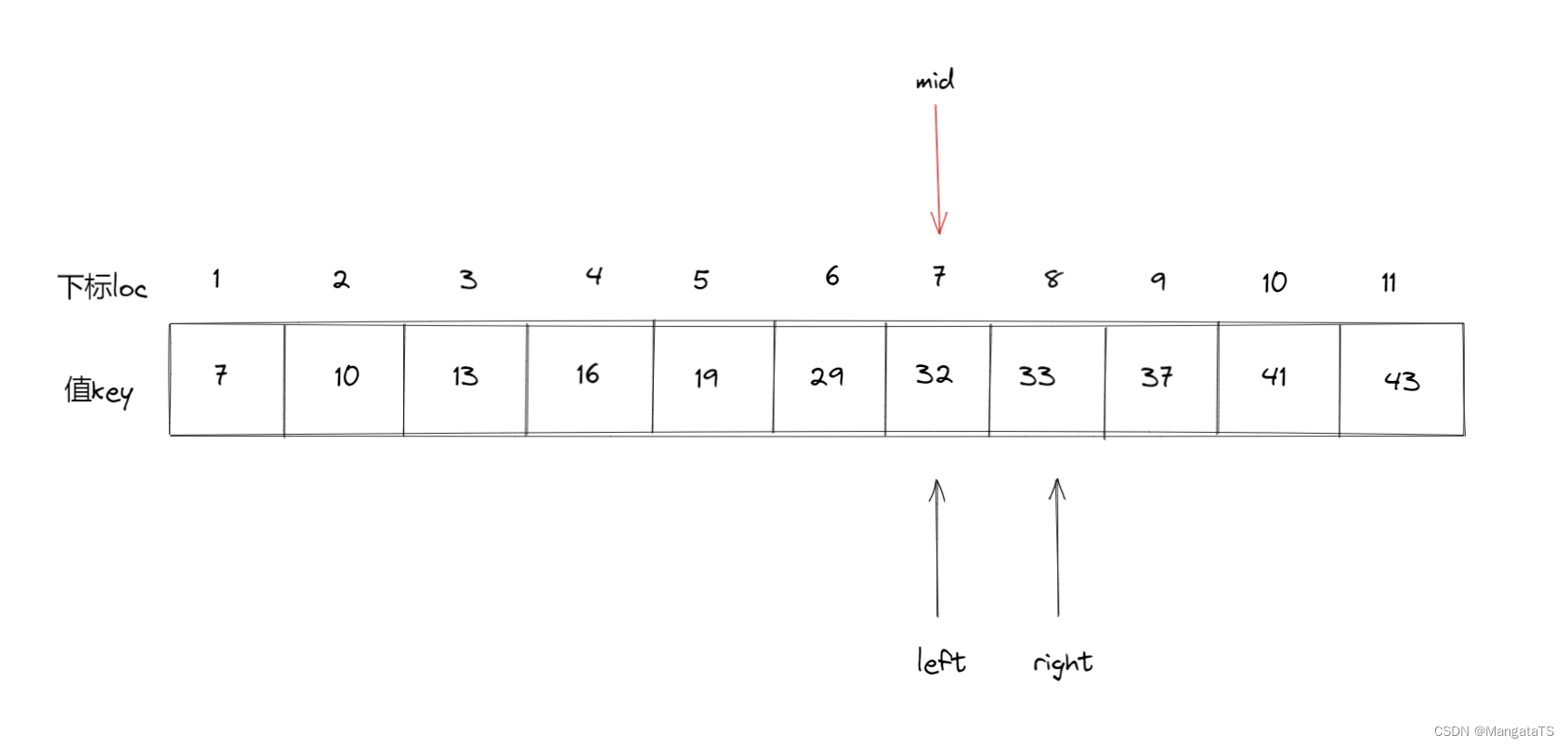
- 第三次查找: \(mid = \left \lfloor \frac{\text{left}+\text{right}}{2} \right \rfloor =\left \lfloor \frac{7+8}{2} \right \rfloor = 7\) 于是我们将 \(a[7]\) 和 \(32\) 进行比较,我们发现 \(a[9] = 32\) 此时我们就找到了这个元素,那么我们将当前位置返回,至此查找完成~
其实二分查找的过程可以看作为一颗二叉树,我们称其为 判定树 , 我们画出上面序列的判定树,不难发现这颗判定树是一颗 平衡二叉树
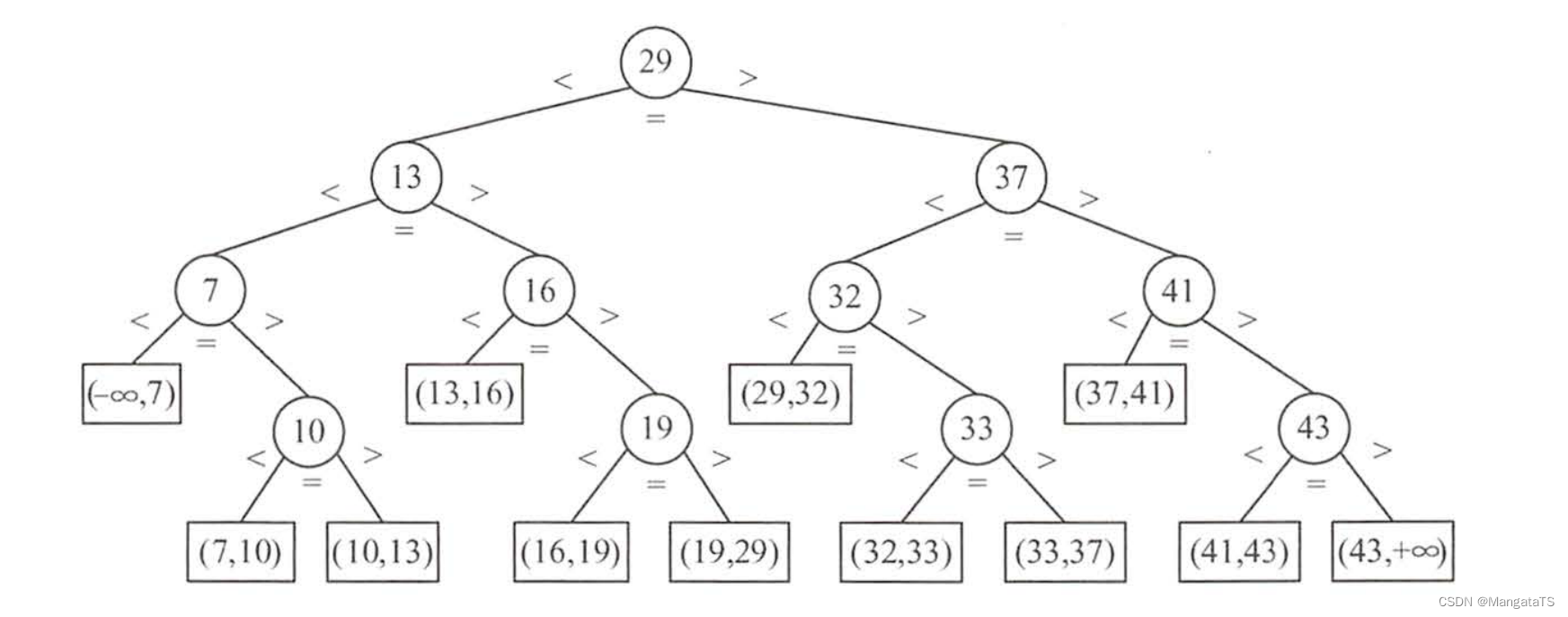
在这棵二叉树中:树中每个圆形结点表示一个记录, 结点中的值为该记录的关键字值;树中最下面的叶结点都是 方形 的,它 表示查找不成功 的情况。
用折半查找法查找到给定值的比较次数最多不会超过 树的高度 。在 等概率 查找时,设 \(h\) 为该判定树的高度,且当树中元素个数为 \(n\) 时判定树高 \(h = \left \lceil log_2(n+1) \right \rceil\) 或者是 \(\left \lfloor log_2(n) \right \rfloor + 1\), 查找成功的平均查找长度为:
对于查找失败的平均长度,也就是到达方框位置的情况,假设有 \(m\) 中情况,且同样为等概率到达,则 \(P_i = \frac{1}{m}\) 假设每一层中的 方形结点数 为 \(D_i\) ,那么就能得到查找失败的平均查找长度为:
2.3 静态树表(次优查找)¶
目前先 pass 不在大纲中,看后面二轮复习有无时间补上空缺~
2.4 索引表(分块查找)¶
2.4.1 基本思想¶
将查找表分为若干子块。 块内的元素可以无序,但块之间是有序的 ,即第一个块中的最大关键字小于第二个块中的所有记录的关键字,第二个块中的最大关键字小于第三个块中的所有记录的关键字,以此类推。再建立一个索引表,索引表中的每个元素含有各块的最大关键字和各块中的第一个元素的地址,索引表按关键字有序排列。
2.4.2 查找步骤¶
- ①第一步是在索引表中确定待查记录所在的块
- ②再块内顺序查找
2.4.3 举例¶
假设我们有这样的查找集合: \(\{88, 24, 72, 61, 21 , 6, 32, 11 , 8, 31, 22, 83, 78, 54\}\)
- 按照关键字我们分为四个块: \(24、54、78、88\)
如下图所示:
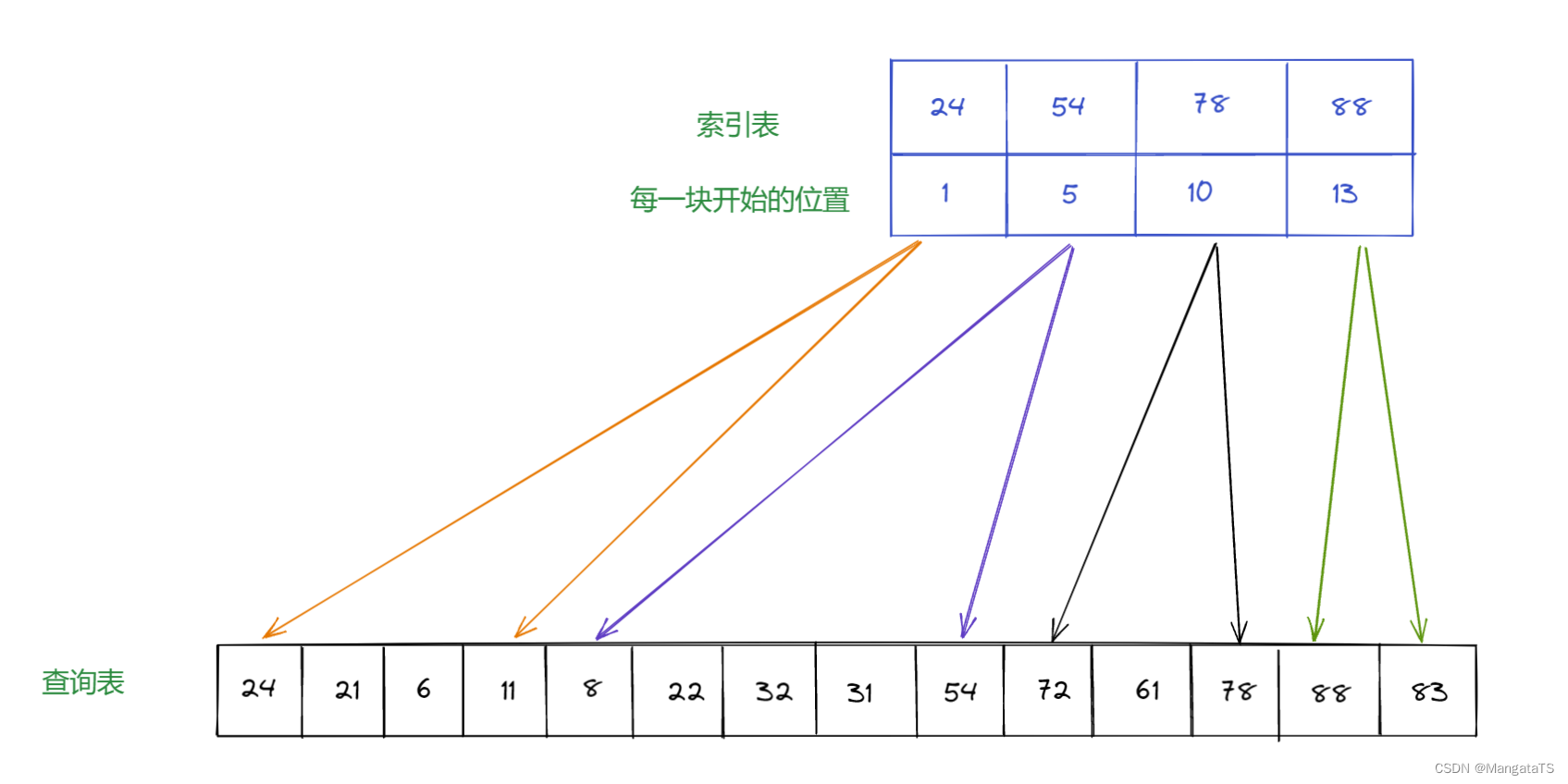
ps:这里的索引表构造可以有多种情况
- 若是我们想要找 \(61\) 那么我们就需要先去在索引表中顺序查找(或是二分查找)我们所需的元素可能出现在哪一块,我们发现 \(61\) 大于第二块表的最大值,并且小于第三块表的最大值,那么 \(61\) 就 可能存在 第三块表中
- 于是我们从下标 \(10\) 开始查找一直到 \(12\) (即这一块的范围),因为表内可能是乱序的,于是我们使用顺序查找的方法,然后找到了 \(61\) 的下标为 \(11\) 这就是一个查找的过程
现在我们接着来分析一下分块查找的平均成功查找长度,很显然这是两个查找过程,索引表查找以及块内查找,那么假设设索引查找和块内查找的平均查找长度分别为 \(Li,Ls\) 那么分块查找的平均成功查找长度为( 因为一般情况下只考虑成功的情况,于是也可以叫做平均查找长度,即忽略了查找失败的情况 ):
将长度度为 \(n\) 的查找表均匀地分为 \(b\) 块, 每块有 \(s\) 个记录,在等概率情况下,若在块内和索引表中均采用顺序查找,则平均查找长度为:
ps:
此时,如果 \(s = \sqrt{n}\) ,那么平均(成功)查找长度取得最小值 \(\sqrt{n}+1\) ,若是对索引表进行二分查找加速的话,那么平均查找长度可为:
三、动态查找¶
3.1 二叉排序树(BST)¶
算法小讲堂之二叉排序树|二叉搜索树|BST:https://acmer.blog.csdn.net/article/details/126607632
3.2 平衡二叉树(AVL)¶
算法小讲堂之平衡二叉树|AVL树(超详细~): https://acmer.blog.csdn.net/article/details/126641989
3.3 B树和B+树¶
算法小讲堂之B树和B+树(浅谈)|考研笔记 :https://acmer.blog.csdn.net/article/details/126688618
3.5 键树(Trie树)¶
Trie (字典)树详解:https://acmer.blog.csdn.net/article/details/120058928
四、哈希表(散列表)¶
算法小讲堂之哈希表|散列表|考研笔记: https://acmer.blog.csdn.net/article/details/126689556