跳转至

AES加密算法

一、简介

AES 算法用来替代原先的DES（ \(Data Encryption Standard\) ），已经被多方分析且广为全世界所使用。经过五年的甄选流程，高级加密标准由美国国家标准与技术研究院 （NIST）于 \(2001\) 年 \(11\) 月 \(26\) 日发布于 \(FIPS PUB 197\) ，并在 \(2002\) 年 \(5\) 月 \(26\) 日成为有效的标准。 \(2006\) 年，高级加密标准已然成为对称密钥加密中最流行的算法之一 。 该算法为比利时密码学家 \(Joan Daemen和Vincent Rijmen\) 所设计，结合两位作者的名字，以 \(Rijdael\) 之名命之，投稿高级加密标准的甄选流程。（ \(Rijdael\) 的发音近于 " \(Rhine doll\) "。）

二、原理

先说明一下无论是明文还是密钥（密钥可以是 \(192\) 、 \(256\) 位，我们这里只考虑 \(128\) 位的情况）还是密文都是 \(128\) 位一组的，也就是16个字节，那么我们就可以用一个 \(4\times 4\) 的矩阵来表示这个数据。

大概的流程可以先看一下这个流程图：（建议看完下面的介绍后再回过来看一下）

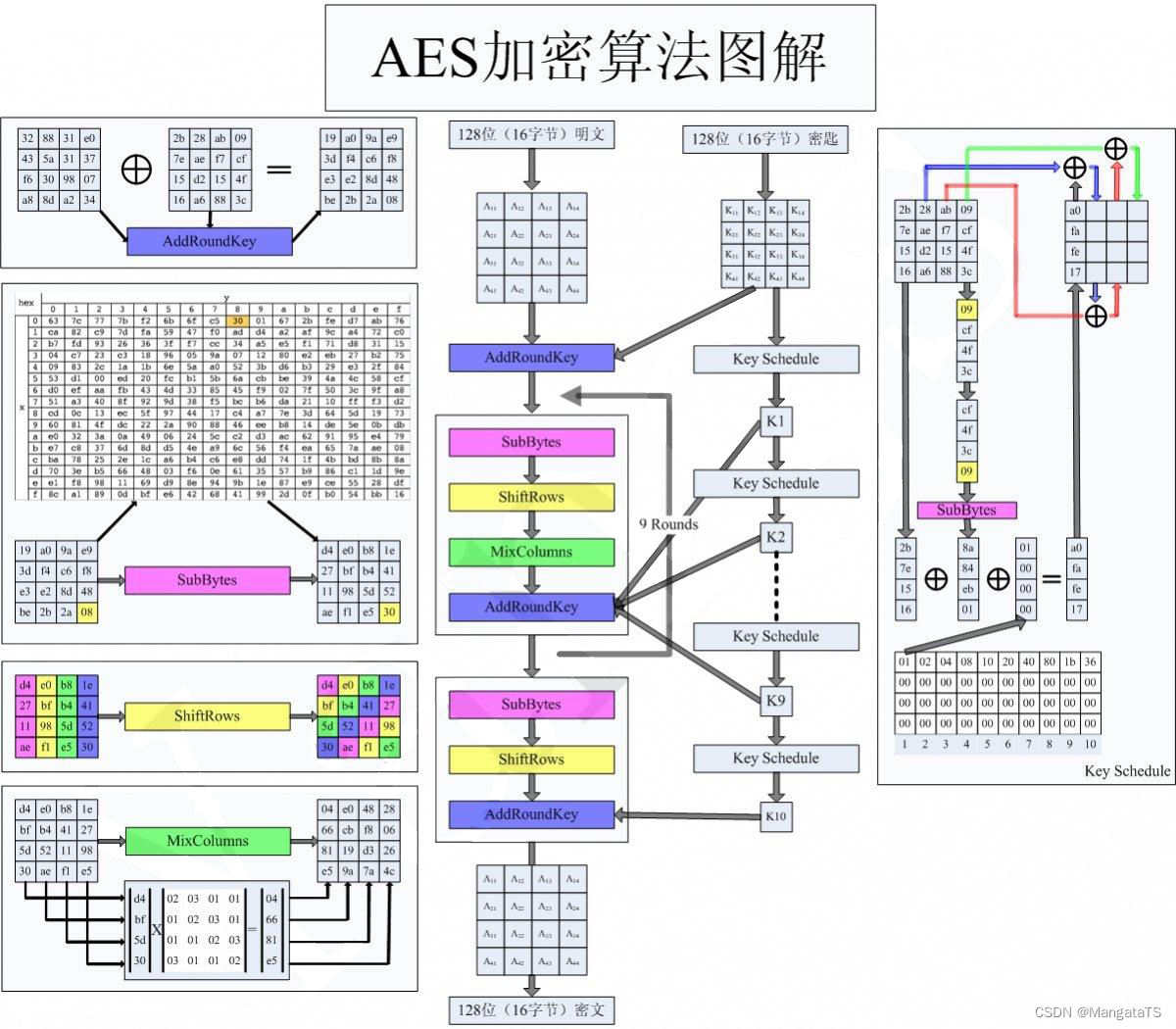
在这里插入图片描述

2.1 明文加密流程

  • 初始变换（其实就是 轮密钥加 操作）
  • 九轮轮函数操作
    • 字节代换（ \(SubBytes\) ）
    • 行位移（ \(ShiftRows\) ）
    • 列混淆 （ \(MixColumns\) ）
    • 轮密钥加（ \(AddRoundKey\) ）
  • 最终轮运算（实际上是 除去 列混淆的轮操作函数）

如图：

在这里插入图片描述

2.2 子密钥生成流程

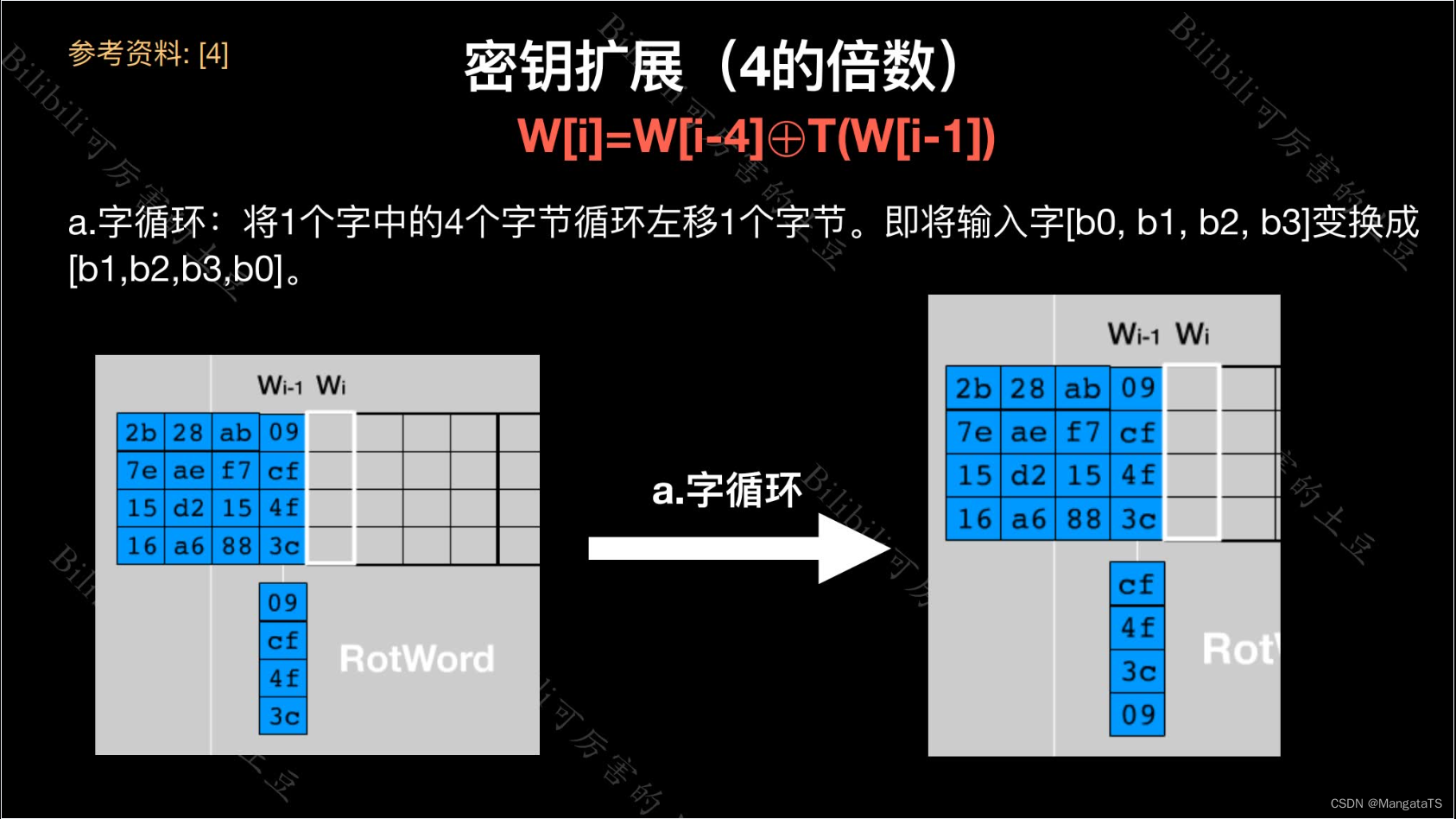
我们的初始密钥也是 \(128\) 位的，那么我们以 一列 作为一个单位进行变化，每新增一个子密钥，我们所谓的列的数量就增加 \(4\) 于是密钥拓展的核心就是：

  • 如果当前拓展的列 \(i\) 不是 \(4\) 的倍数，那么第 \(i\) 列由如下等式确定：（其中 \(W[i]\) 表示的就是第 \(i\) 列的数据）
\[ W[i]=W[i-4] \ Xor \ W[i-1] \]
  • 如果当前拓展的列 \(i\) 是 \(4\) 的倍数，那么第 \(i\) 列由如下等式确定：
\[ W[i]=W[i-4] \ Xor \ T(W[i-1]) \]

关于这个 \(T\) 函数，我们下面仔细讲解

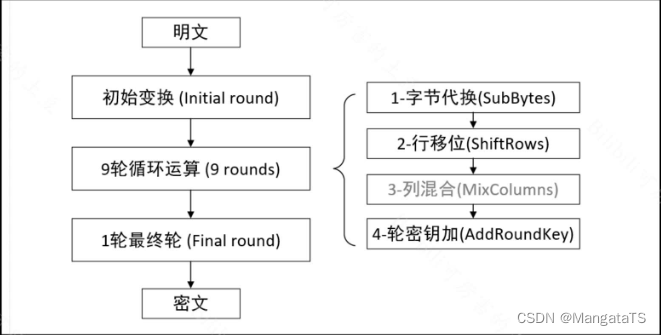
2.3 字节代换

一般来说我们会给一个 \(16\times 16\) 的 \(S\) 盒子，然后我们将每一个字节的前 \(4\) 位（转化为16进制）作为 \(X\) 轴的坐标，然后后 \(4\) 位作为 \(Y\) 轴的坐标，然后进行一个值的替换，最终我们将所有字节都替换完成即可

这里借用一个图：

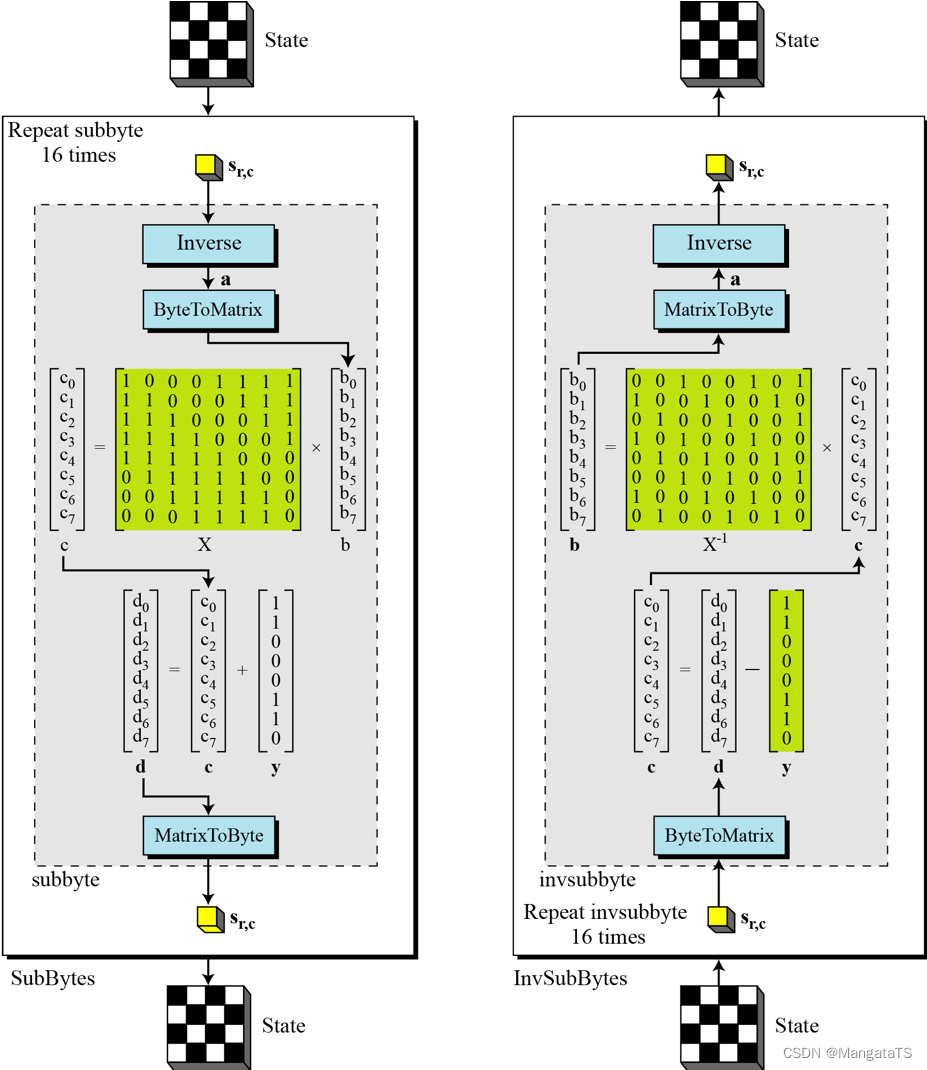
在这里插入图片描述

2.4 行位移

此时我们需要将每一行数据想象成一个环形

  • 对于第一行，我们保持不变
  • 对于第二行，我们向左循环移动 \(1\) 个字节
  • 对于第三行，我们向左循环移动 \(2\) 个字节
  • 对于第四行，我们向左循环移动 \(3\) 个字节

可以参考下图：

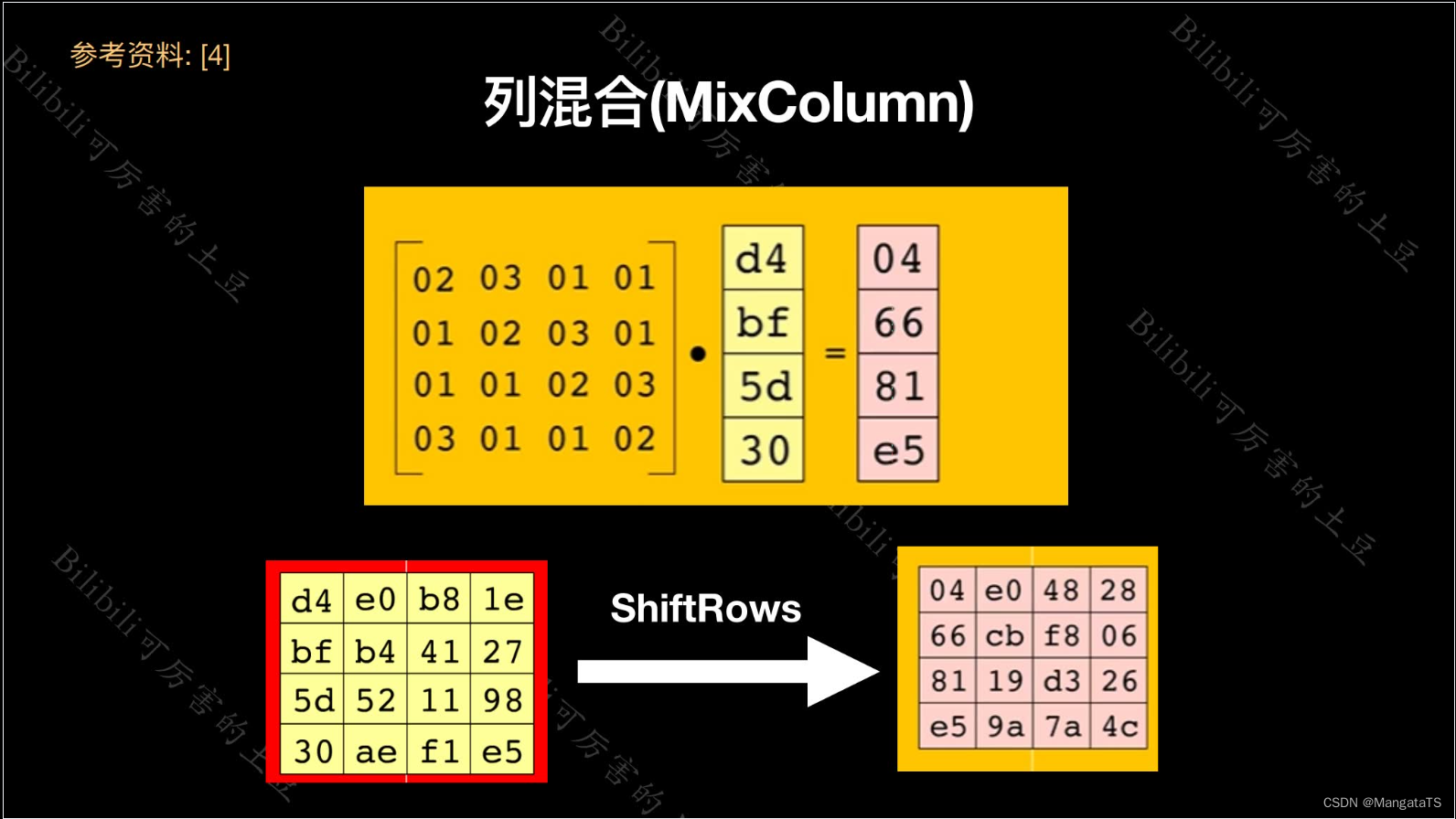
在这里插入图片描述

2.5 列混淆（混合）

我们将会给当前的这个矩阵 左乘 一个 指定矩阵 但是注意的是这里的矩阵乘法不是普通意义上的，而是有限域 \(GF(2^8)\) 上的乘法，我们知道矩阵的乘法是左边的行乘上右边的列，那么对于每一个字节而言，都有 \(8\) 位，在有限域的乘法中，乘法变为了多项式乘法，例如：

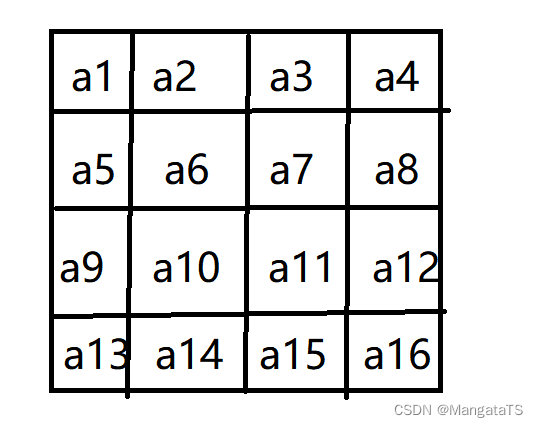在这里插入图片描述 然后加法变成了异或运算，例如，我们现在左边矩阵第一行的元素都是 \(a_i\) ，右边的矩阵元素都是 \(b_i\) ，顺序如下：

在这里插入图片描述 B矩阵同理，那么我们想算出新矩阵 \(C\) 的第一个字节的值就为：

\[ c_1 = (a_1 \times b_1) ⊕ (a_2 \times b_5) ⊕ (a_3 \times b_9) ⊕ (a_4 \times a_{13}) \]

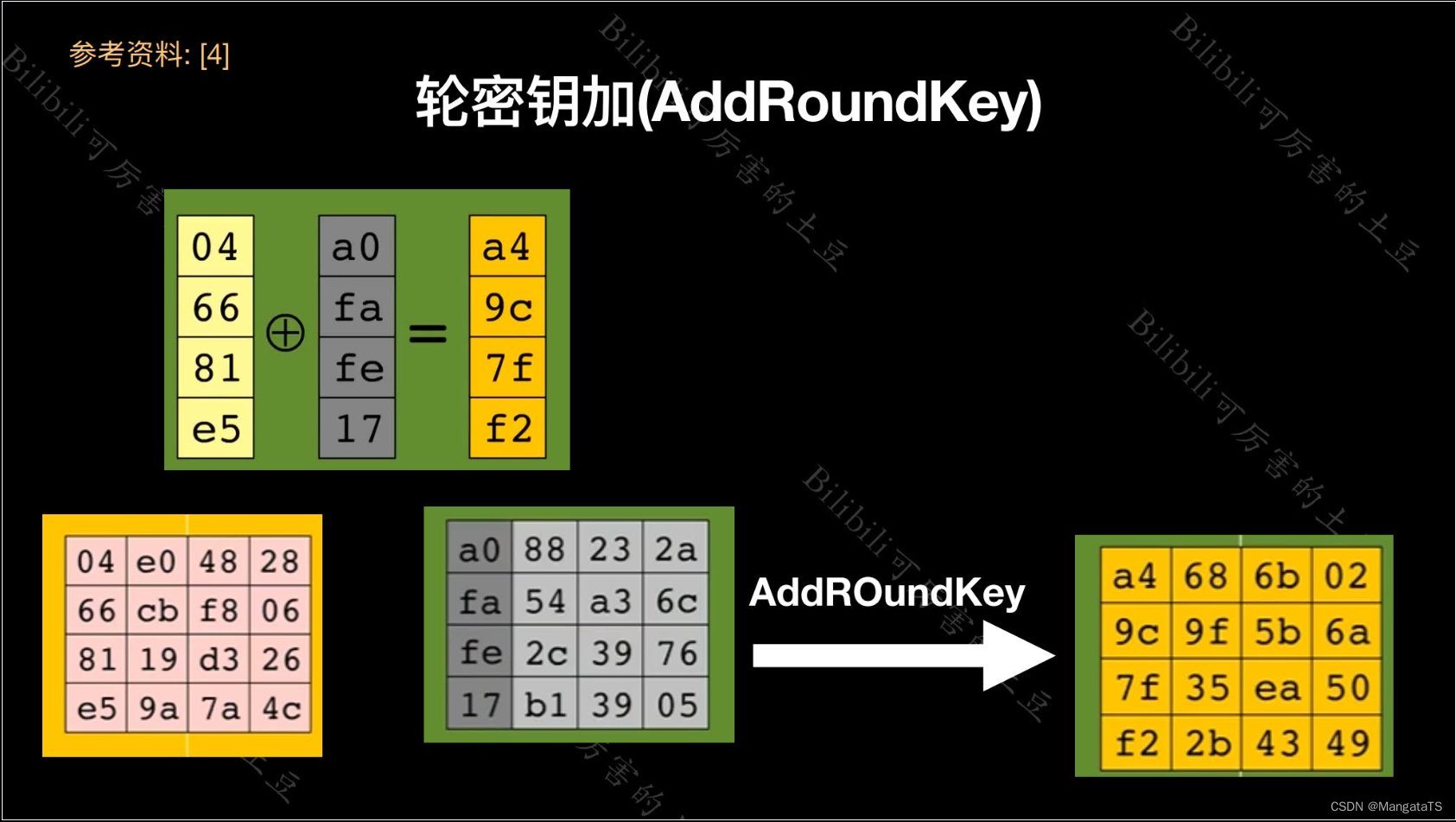
在这里插入图片描述

2.6 轮密钥加变换

轮密钥加就是直接将一个 指定矩阵 和当前的待加密矩阵进行对每个字节 按位异或 操作即可

大概操作如图：

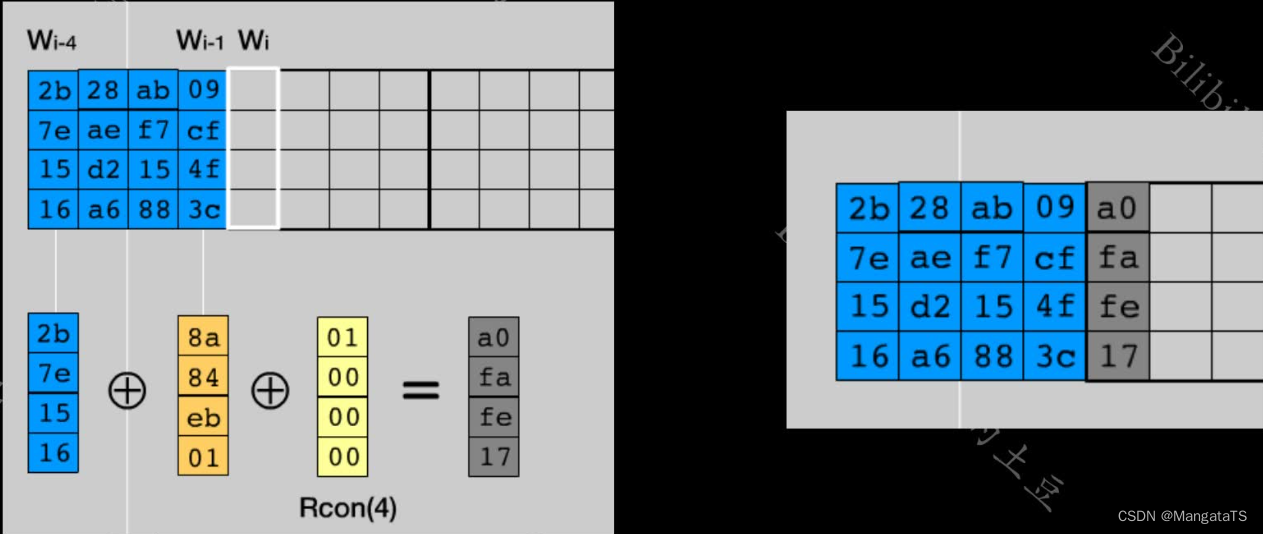
在这里插入图片描述

2.7 密钥拓展中的T函数

\(T\) 函数由三个部分组成： 字循环 、 字节代换 、 轮常量异或

2.7.1 字循环

在这里插入图片描述

2.7.2 字节代换

这里的代换和上面提到的是一样的，就是 \(S\) 盒子代换，前 \(4\) 位 作为查找的 \(X\) 坐标，后 \(4\) 位作为查找的 \(Y\) 坐标，然后再盒子（字节表）中查找替换即可

2.7.3 轮常量异或

将前两步的结果同轮常量 \(Rcon[j]\) 进行异或操作，其中的 \(J\) 表示的是轮数，注意的是这里的轮常量是 给定的 ，这样我们会发现，如果说当前的列数是 \(4\) 的倍数的时候，我们需要进行 两次 列异或操作

在这里插入图片描述

三、优缺点

3.1 优点

  • 安全性高，稳定的数学基础、没有算法弱点、算法抗密码分析强度高
  • 性能好，能在多个平台上以较快的速度实现
  • 存储空间小，不能占用大量的存储空间和内存
  • 灵活性、硬件、软件适应性、算法的简单性等
  • 很好的抵抗差分密码分析及线性密码分析的能力。
  • AES的密钥长度比DES大，它也可设定为32比特的任意倍数，最小值为128比特，最大值为256比特，所以用穷举法是不可能破解的。

3.2 缺点

目前尚未存在对AES 算法完整版的成功攻击，但已经提出对其简化算法的攻击。

四、对比DES

4.1 相同之处

  • 两者的轮函数都是由三部分构成，非线性层、线性混合层、子密钥异或，只不过顺序不同
  • AES的子密钥异或对应于DES的 \(S\) 盒子之前的子密钥异或
  • AES的列混淆运算的目的是为了让不同的字节相互影响，而DES中F函数的输出于左边一半数据相加也有类似的效果
  • AES的非线性运算是字节代替（ByteSub），对应于DES中的非线性运算 \(S\) 盒子
  • 行位移运算保证了每一行的字节不仅仅影响其他行对应的字节，而且影响其他行所有的字节，这与 DES 中的置换 \(IP\) 相似

4.2 不同之处

  • AES 的密钥长度（ \(128\) 位、 \(192\) 位、 \(256\) 位）是可变的，而 DES 的密钥固定长度为 \(56\) 位
  • DES 是面向比特运算的，而 AES 是面向字节运算的
  • AES的加密运算和解密运算不一致，因而加密器不能同时作为解密器，而DES则无此限制

五、代码实现

留坑（但是感觉不会填，后面看情况吧）

最后更新: 2022-09-18 12:08:00

评论

回到页面顶部