拓扑排序¶
一、前言¶
AOV网：若用 \(DAG\) 图表示一个工程，其顶点表示活动，用有向边 \(＜V_i ,V_j＞\) 表示活动 \(V_i\) 只必须先于活动 \(V_j\) 进行的这样一种关系，则将这种有向图称为顶点表示活动的网络，记为 \(AOV\) 网
将一个 有向无环图（DAG）所有顶点线性化的算法就是 拓扑排序 ，当然啦这个序列显然满足以下两个条件： - 图中每个顶点仅出现一次 - 若点 \(A\) 在图中有一个指向点 \(B\) 的弧，那么在序列中 \(A\) 一定在 \(B\) 的前面
二、原理¶
对于一个 \(AOV\) 网我们进行排序的算法有很多，这里主要介绍 \(Kahn\) 算法，算法步骤如下：
- ①从 \(AOV\) 网中选择一个没有前驱的顶点（ 入度为0 ）并输出
- ②从 \(AOV\) 网中 删除 该顶点以及该顶点相关的有向边
- 重复步骤①、②直到当前的 \(AOV\) 网为空 或者当前网中 不存在无前驱的结点 为止，而后一种情况就说明了图中存在环
举个例子，假设有如下的 \(DAG\) 图：
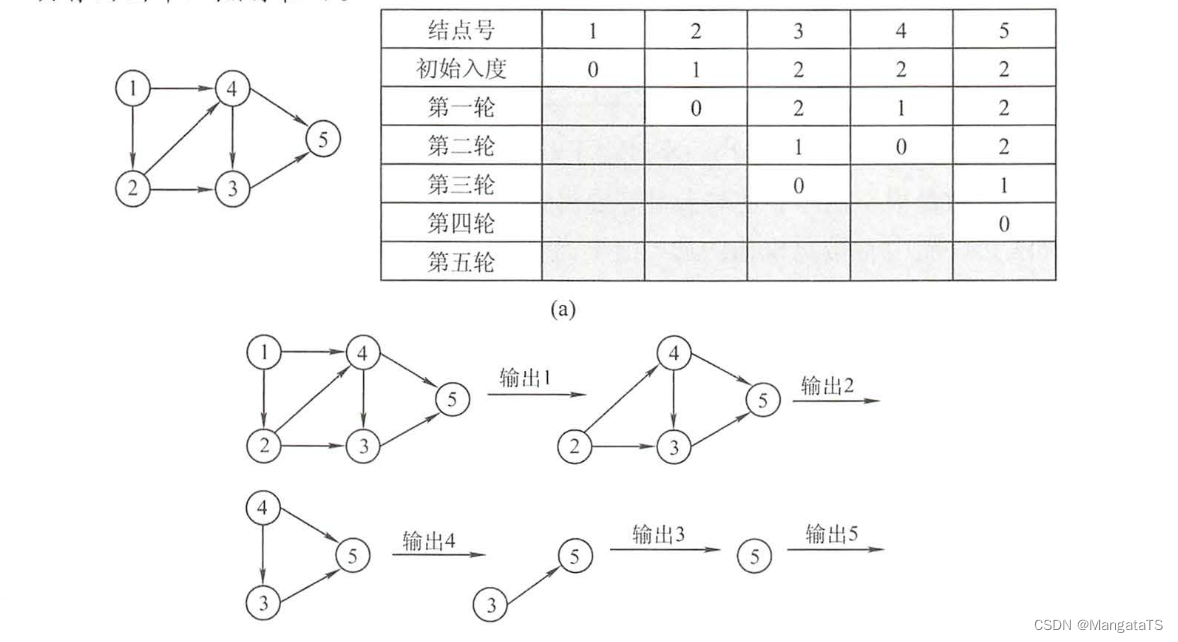我们可以看到在第一轮删除了①号结点，然后接着是②、④、③、⑤，每次删除结点以及和这个结点相关的边，都会让这个结点指向的下一个结点的入度减一
注意：一个 \(DAG\) 图可能存在多个拓扑排序，例如下图的拓扑排序
我们发现这里的拓扑排序可能是：\([①、②、③、④、⑤]\) 也有可能是 \([①、③、②、④、⑤]\)
三、代码实现¶
从上面的步骤来看，这个拓扑排序需要记录每个点的度数，我们可以用一个数组 \(d\) 记录每个点的入度，读完图后（读图的过程中记录每个点的入度），我们将入度为 \(0\) 的点先放入队列 que 中，然后不断地取出队首元素，并放进我们的序列数组ans中，然后将队首元素出度的边都删掉，也就是将边连接的这些点的入度减一，如果发现入度减为 \(0\) 了，那么就将这个点加入队列中，然后重复这个操作就能得到拓扑排序的结果啦
#include<bits/stdc++.h>
using namespace std;
//----------------自定义部分----------------
#define ll long long
#define mod 1000000007
#define endl "\n"
#define PII pair<int,int>
#define INF 0x3f3f3f3f
const int N = 2e6+10;
//----------------自定义部分----------------
int n,m,q,d[N],vis[N];
vector<int> V[N],ans;
bool topsort(){
queue<int> que;
for(int i = 1;i <= n; ++i) {
if(!d[i]) que.push(i);
}
while(!que.empty()){
int t = que.front();
que.pop();
ans.push_back(t);
for(int i = 0,l = V[t].size();i < l; ++i){
d[V[t][i]]--;
if(!d[V[t][i]]) que.push(V[t][i]);
}
}
return ans.size()==n;
}
void slove(){
if(topsort()){
for(int i = 0;i < n; ++i) {
cout<<ans[i]<<" \n"[i==n-1];
}
}
else{
cout<<"-1"<<endl;
}
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
cin>>n>>m;
int u,v;
for(int i = 0;i < m; ++i) {
cin>>u>>v;
V[u].push_back(v);
d[v]++;
}
slove();
return 0;
}
很显然，如果我们发现得到的序列的个数和图的点数不同的话就说明图中存在环，不能构成拓扑排序
四、应用¶
4.1 判环¶
这是一个很显然的应用，如果构不成线性序列，则说明该图不是一个 \(DAG\) 图，即图中存在环
4.2 处理依赖性任务规划问题¶
一个很常见的依赖性问题就是学习学科，假设有学科 \(A、B、C、D\) 其中的关系为，学习学科 \(B\) 则需要有学科 \(A\) 的基础，学习学科 \(C\) 也需要学科 \(A\) 的基础，而学习学科 \(D\) 则需要学科 \(B、C\) 的基础，那么这个学科关系很显然就是一个 \(DAG\) 图，关系如下：
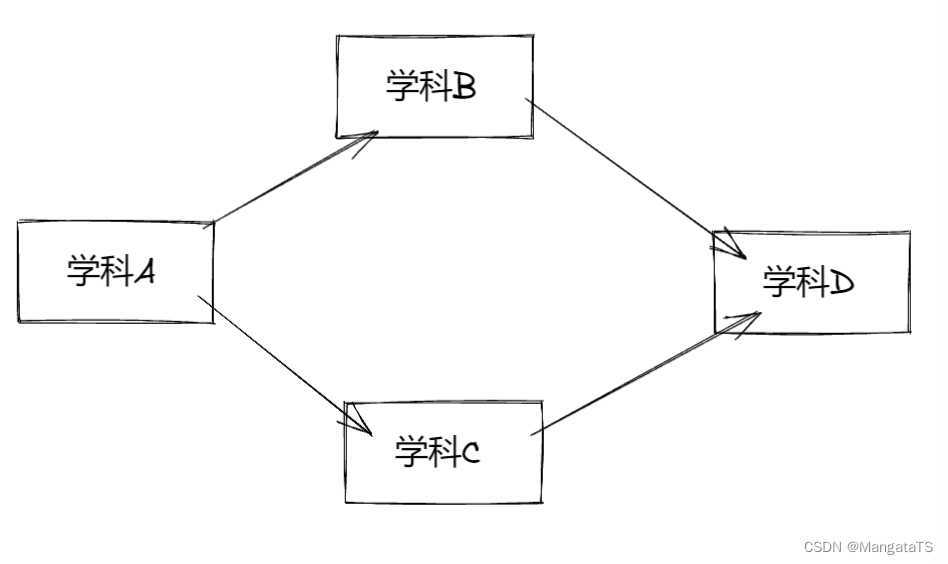假设我们想知道这个学科学习的线性关系，那么这个问题就是 拓扑排序 了
4.3 求解关键路径¶
拓扑排序可以用在关键路径算法的求解上，能通过拓扑排序求出 最早开始时间 以及通过逆拓扑排序求出 最迟开始时间
五、练习题¶
题目：https://acm.hdu.edu.cn/showproblem.php?pid=1285 题解：https://acmer.blog.csdn.net/article/details/123826423
题目：https://acm.hdu.edu.cn/showproblem.php?pid=2647 题解：https://acmer.blog.csdn.net/article/details/123831552