希尔加密算法¶
一、简介¶
Hill密码又称希尔密码是运用基本矩阵论原理的替换密码,属于多表代换密码的一种,由 \(Lester S. Hill\) 在1929年发明。
随着科技的日新月异和人们对信用卡、计算机的依赖性的加强,密码学显得愈来愈重要。密码学是一门关于加密和解密、密文和明文的学科。若将原本的符号代换成另一种符号,即可称之为广义的密码。狭义的密码主要是为了保密,是一种防止窃文者得知内容而设的另一种符号文字,也是一般人所熟知的密码。 使用信用卡、网络账号及密码、电子信箱、电子签名等都需要密码。为了方便记忆,许多人用生日、电话号码、门牌号码记做密码,但是这样安全性较差。 为了使密码更加复杂,更难解密,产生了许多不同形式的密码。密码的函数特性是明文对密码为一对一或一对多的关系,即明文是密码的函数。传统密码中有一种叫移位法,移位法基本型态是加法加密系统 \(C=P+s(mod \ m)\) 。一般来说,我们以 \(1\) 表示 \(A,2\) 表示 \(B,……,25\) 表示 \(Y\), \(26\) 表示Z,以此类推。由于 \(s=0\) 时相当于未加密,而 \(0≤s≤m-1\)( \(s≥m\) 都可用 \(0≤s≤m-1\) 取代),因此,整个系统只有 \(m-1\) 种变化。换言之,只要试过 \(m-1\) 次,机密的信息就会泄漏出去。 由此看来,日常生活中的密码和传统的密码的可靠性较差,我们有必要寻求一种容易将字母的自然频度隐蔽或均匀化,从而有利于统计分析的安全可靠的加密方法。 希尔密码能基本满足这一要求 。
二、原理¶
2.1 Hill加密原理¶
- 对于每一个字母,我们将其转化为对应的数字,一般来说我们使用的是 \(A\) 对应的 \(0\) ,\(B\) 对应的 \(1\) 然后一次类推,当然你也可以自己指定一个字母表,然后一一对应
- 我们将明文转化为一个 \(1\) 维的向量 (即:\(1\times n\) 的矩阵)
- 然后我们将这个 \(1\) 维的向量和一个 \(n\times n\) 的密钥矩阵相乘,得到一个 \(1\) 维的向量,然后对这个矩阵模上 \(26\)
- 然后再通过字母表将这个 \(n\) 维矩阵转化为密文
解密 的话只需要将密文乘上密文矩阵的 逆矩阵 就好啦, Hill 密码能较好地抵抗统计分析法,对抗唯密文攻击的强度较高,但易受到已知明文攻击。破译的难度也会随着矩阵的阶数规模变大变得难以破解
2.2 矩阵求逆原理¶
在上一篇博客中降到了关于矩阵求逆的高斯消元方法: 传送门:https://acmer.blog.csdn.net/article/details/125012646
三、 举例¶
我们的明文为:ACM,我们想将其加密,我们得到的一个密钥矩阵如下:
- 我们将明文转为一个 \(1\) 维向量:
- 对两个矩阵做一个乘法
- 将新得到的 \(1\) 维向量按照字母表转化为密文:

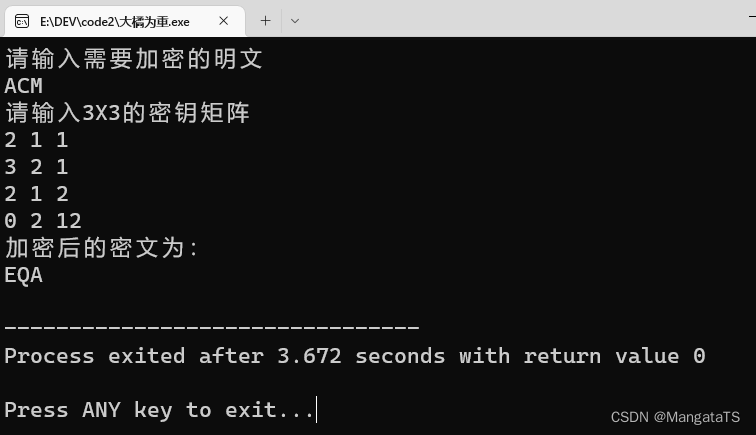
得到密文:EQA
四、代码¶
4.1 加密代码¶
#include<bits/stdc++.h>
using namespace std;
#define N 100
#define mod 26
struct Matrix{
int n,m;
int mp[N][N];
void init(int n,int m) {
this->n = n;
this->m = m;
for(int i = 0;i <= n; ++i)
for(int j = 0;j <= m; ++j)
mp[i][j] = 0;
}
};
Matrix mult(Matrix L,Matrix R) {//乘法
if(L.m != R.n) return L;
Matrix M;
M.init(L.n,R.m);
for(int i = 0;i < L.n; ++i) {
for(int j = 0;j < R.m; ++j){
for(int k = 0;k < L.m; ++k) {
M.mp[i][j] = (M.mp[i][j] + L.mp[i][k] * R.mp[k][j]) % mod;
}
}
}
return M;
}
void HIll(){
Matrix a,b;
string S;
cout<<"请输入需要加密的明文"<<endl;
cin>>S;
transform(S.begin(),S.end(),S.begin(), ::toupper);
int len = S.size();
cout<<"请输入"<<len<<"X"<<len<<"的密钥矩阵"<<endl;
a.init(len,len);
b.init(1,len);
for(int i = 0;i < len; ++i)
for(int j = 0;j < len; ++j)
scanf("%d",&a.mp[i][j]);
for(int i = 0;i < len; ++i)
b.mp[0][i] = int(S[i] - 'A');
for(int i = 0;i < len; ++i)
cout<<b.mp[0][i]<<" \n"[i == len-1];
Matrix c = mult(b,a);
string ans = "";
for(int i = 0;i < len; ++i)
ans += char('A' + c.mp[0][i]);
cout<<"加密后的密文为:\n"<<ans<<endl;
}
int main()
{
HIll();
return 0;
}
/*
ACM
2 1 1
3 2 1
2 1 2
ans = EQA
----------------
ACT
6 24 1
13 16 10
20 17 15
ans = QRT
----------------
cyber
10 5 12 0 0
3 14 21 0 0
8 9 11 0 0
0 0 0 11 8
0 0 0 3 7
ans = WRTRV
*/
4.2 解密代码¶
由于矩阵求逆用的是浮点高斯,那么有可能逆矩阵就是一个浮点数或者,所以至于要怎么处理(四舍五入、向上向下取整)就取决于需求者了,所以我这里也就不放出代码了,道理明白就行。