AVL平衡树¶
一、前言¶
通过前面的二叉排序树的学习（传送门：https://acmer.blog.csdn.net/article/details/126607632），我们发现了一个问题，如果说数据的插入顺序是一个有序的，那么这个二叉排序树就会退化成链状，这就导致了二叉排序树的查找速度直接变为 \(O(N)\) 那这就和线性表没啥区别了，有没有什么办法能让这个二叉树最好一直稳定在 “最佳状态”呢 那么就要引出今天的主角： 平衡树（AVL树） 了，其实 \(AVL\) 树的原理非常简单，在正常二叉排序树的操作中只是多加入了四种旋转子树的操作使得这颗二叉树的 高度 尽量保持平衡（即不让树的高度增长过快）
二、定义¶
平衡二叉树，又称 \(AVL\) 树，它是一种 特殊的 二叉排序树。AVL树或者是一棵空树，或者是具有以下性质的二叉树：
- 左右子树都是一颗平衡树
- 左子树和右子树的深度（高度）之差的绝对值不超过 \(1\)
对于每一个分支节点，左右子树的高度差就为该节点的 平衡因子 ，显然对于每一个叶结点高度差为 \(0\) ，例如下图两颗分别为平衡和非平衡树：
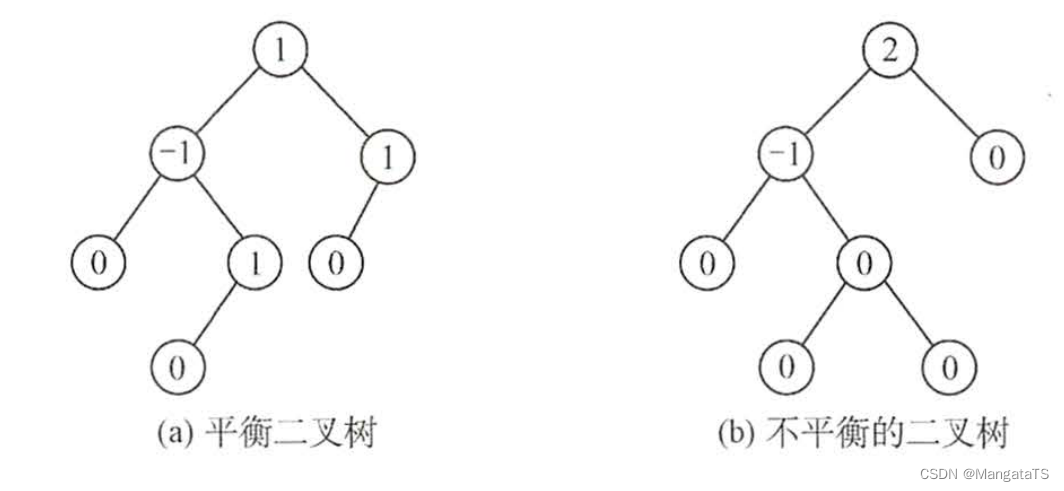其中结点的值就是该结点的 平衡因子
三、原理¶
首先是对于二叉树的结点定义，对于这个结点我们需要比之前的二叉排序树多一个值就是 height 用于记录当前结点的高度，所以得到结点的定义如下：
template<typename T>
class AvlNode {
public:
T key;
int height;
AvlNode *left,*right;
AvlNode(int key) {
this->key = key;
this->height = 0;
this->left = this->right = NULL;
}
~AvlNode() {
}
};
template<typename T>
class AvlTree {
public:
AvlNode<T> *root;
AvlTree() {
this->root = NULL;
}
//获取树结点的高度
int GetHeight(AvlNode<T> *root);
//更新树结点的高度
int MaxHeight(AvlNode<T> *root);
//判断是否失去平衡，失去平衡返回true，否则返回false
bool Check_Balance(AvlNode<T> *a, AvlNode<T> *b);
//简称为LL旋转（LL的含义是左子树的左子树插入新结点）
AvlNode<T>* LeftLeftRotate(AvlNode<T> *root);
//简称为RR旋转（RR的含义是右子树的右子树插入新结点）
AvlNode<T>* RightRightRotate(AvlNode<T> *root);
//简称为LR旋转（LR的含义是左子树的右子树插入新节点）
AvlNode<T>* LeftRightRotate(AvlNode<T> *root);
//简称为RL旋转（RL的含义是右子树的左子树插入新节点）
AvlNode<T>* RightLeftRotate(AvlNode<T> *root);
//在AVL树中查找元素值为value的结点
AvlNode<T>* ValueFind(AvlNode<T> *root,T value);
//找到AVL树中元素值最小的结点，即树的最左边
AvlNode<T>* MinNode(AvlNode<T> *root);
//找到AVL树中元素值最大的结点，即树的最右边
AvlNode<T>* MaxNode(AvlNode<T> *root);
//在AVL树中插入元素值为T的结点
AvlNode<T>* InsetNode(AvlNode<T> *root,T value);
//删除结点
AvlNode<T>* DeleteNode(AvlNode<T> *root, AvlNode<T> *node);
//先序遍历
void PreOrder(AvlNode<T> *root) {
if(root == NULL) return;
std::cout<<root->key<<"->";
PreOrder(root->left);
PreOrder(root->right);
}
//中序遍历
void InOrder(AvlNode<T> *root) {
if(root == NULL) return;
InOrder(root->left);
std::cout<<root->key<<"->";
InOrder(root->right);
}
//后序遍历
void PostOrder(AvlNode<T> *root) {
if(root == NULL) return;
PostOrder(root->left);
PostOrder(root->right);
std::cout<<root->key<<"->";
}
};
其中三种遍历方式是为了后面校验平衡二叉树的形态是否正确，前三个函数：
int GetHeight(AvlNode<T> *root)：传入一个二叉树的结点，然后我们返回这个二叉树结点的height成员变量，但是我们传入的结点可能是NULL直接去取元素的话会发生RE所以我们需要先判断一下int MaxHeight(AvlNode<T> *root);：其实叫UpdataHeight更为合理，是用于更新当前结点的高度的函数bool Check_Balance(AvlNode<T> *a, AvlNode<T> *b);：传入两个结点，判断一下以他们分别作为根结点的子树的高度是否发生失衡，如果失衡那么就返回true否则返回false
3.1 查找操作¶
前面说了只有树形结构发生变化的时候才会导致二叉树失去平衡，那么显然只有是插入和删除结点的操作的时候才可能发生，所以对于查找的操作来说和前面的平衡二叉树是相同的，代码如下：
template<typename T>
AvlNode<T>* AvlTree<T>::ValueFind(AvlNode<T> *root,T value) {
//如果当前走到了空结点或者找到了value值的结点都会退出，前者说明找不到
while(root != NULL && root->key != value) {了，后者说明找到了
if(root->key > value)
root = root->left;//在左子树
else
root = root->right;//在右子树
}
return root;//没找到的话会返回NULL
}
3.2 最小（大）值结点¶
- 最大值结点就是在整棵树的最右边，也就是从根节点出发一直往右子树走，直到某个结点的右儿子为
NULL此时就找到了，代码如下：template<typename T> AvlNode<T>* AvlTree<T>::MaxNode(AvlNode<T> *root) { if(root == NULL) //特判一下空树的情况 return NULL; if(root->right == NULL) //当结点的右子树为空，说明找到了 return root; return MaxNode(root->right);//递归往右子树查找 } - 最小值结点和最大值同理，从根节点出发一直往左子树走，直到某个结点的左儿子为
NULL，此时就找到了，代码如下：template<typename T> AvlNode<T>* AvlTree<T>::MinNode(AvlNode<T> *root) { if(root == NULL) return NULL;//特判一下空树的情况 if(root->left == NULL) //当结点的左子树为空，说明找到了 return root; return MinNode(root->left); }
3.3 旋转操作¶
平衡二叉树最重要最核心的操作也就是旋转操作了，总体分为四种旋转操作，即 \(LL\) 旋转 、\(RR\) 旋转、 \(LR\) 旋转、 \(RL\) 旋转，这里的定义其实是很有关系的，我们一一来讲解，先放两张失衡 \(AVL\) 树的图，结合下面的定义以及实现观看：
case1:
case2:
3.3.1 LL旋转¶
-
发生情况： 这里的
LL指的是指通过在最低失去平衡的结点的左子树的左子树插入结点，导致失衡所要做出的旋转，当然若是失衡结点的右子树结点被删除也有可能造成LL旋转，因为就等同左子树的左子树插入结点 -
操作： 当发生
LL失衡的时候，我们可以简单将这颗 \(AVL\) 抽象成如下图所示：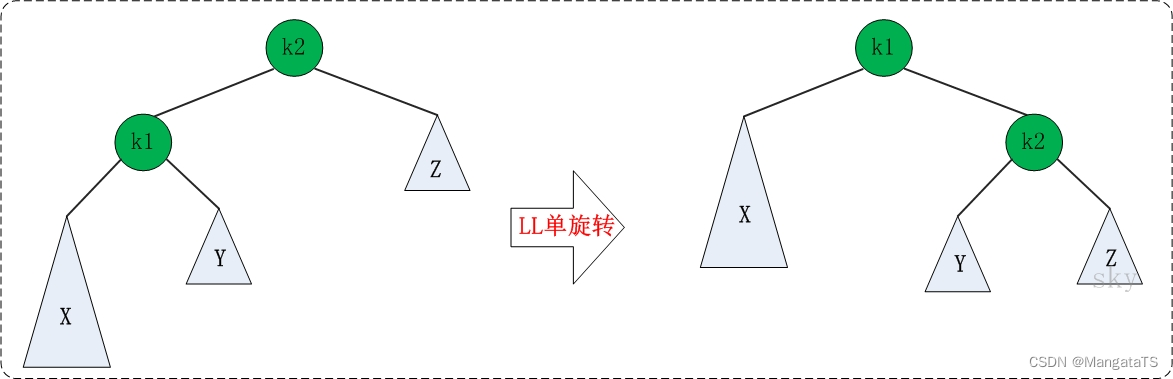
可以简单分为四步： - 将左子树的右子树（Y）变为根（K2）的左子树
- 将左子树的根结点 \(k1\) 变为整个子树的根结点，然后让其右子树指针指向之前的根 \(k2\)
- 更新 \(k1\) 和 \(k2\) 的高度
- 将旋转后的新根（ \(k1\) ）返回
比如插入序列为：\(\{5,6,3,2,4,1 \}\) 的时候，此时以 \(5\) 为根节点的位置的左子树发生了失衡，然后我们对其进行LL旋转将左儿子结点旋转到根节点的位置，如下图所示：
步骤明白后，代码其实也就很简单了：
template<typename T>
AvlNode<T>* AvlTree<T>::LeftLeftRotate(AvlNode<T> *root) {
AvlNode<T> *lchild = root->left;//记录一下左子树根结点
root->left = lchild->right;//将左子树的右子树变为根的左子树
lchild->right = root;//将左子树的根变为整个树的根，然后让其右子树指向之前的根
//更新一下当前子树的根结点的高height
lchild->height = MaxHeight(lchild);
//更新一下被旋下去的结点，即当前子树的根的右子树结点的高height
root->height = MaxHeight(root);
return lchild;//返回子树旋转后的新的根
}
实际上我们说对某一个结点做LL旋的话，其实就是想将那个结点 往右旋转
3.3.2 RR旋转¶
-
发生情况： 这里的
RR指的是指通过在最低失去平衡的结点的右子树的右子树插入结点，导致失衡所要做出的旋转，当然若是失衡结点的左子树结点被删除也有可能造成RR旋转，因为就“等同右子树的右子树插入结点” -
操作： 当发生
RR失衡的时候，我们可以简单将这颗 \(AVL\) 抽象成如下图所示：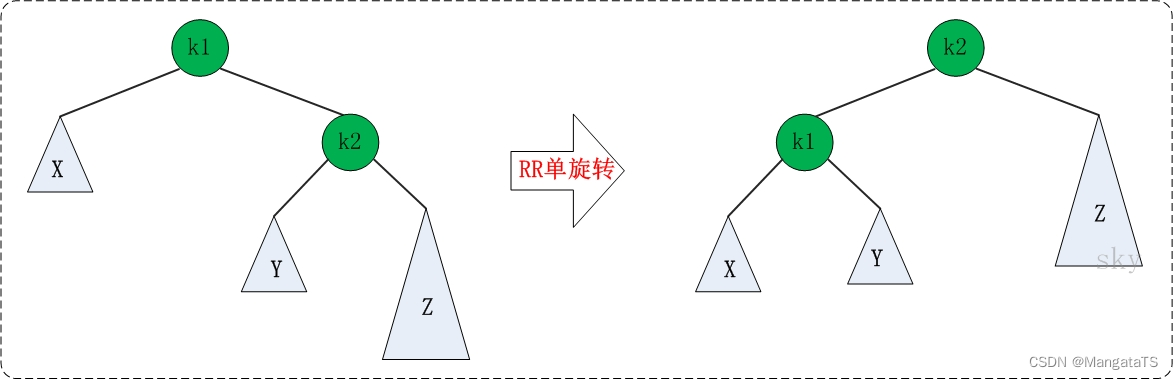
其实你会发现 \(RR\) 单旋转是和前面的 \(LL\) 单旋转其实是对称的，那么操作步骤仍然是四步： - ①将右子树的左子树（Y）变为根（K1）的左子树
- ②将左子树的根结点 \(k2\) 变为整个子树的根结点，然后让其左子树指针指向之前的根 \(k1\)
- ③更新 \(k1\) 和 \(k2\) 的高度
- ④将旋转后的新根（ \(k2\) ）返回
比如插入序列为：\(\{2,1,4,5,3,6 \}\) 的时候，此时以 \(2\) 为根节点的位置的右子树发生了失衡，然后我们对其进行RR旋转将右儿子结点旋转到根节点的位置，如下图所示：
代码如下：
template<typename T>
AvlNode<T>* AvlTree<T>::RightRightRotate(AvlNode<T> *root) {
AvlNode<T> *rchild = root->right;//记录一下右子树根结点
root->right = rchild->left;//将右子树的左子树变为根的右子树
rchild->left = root;//将右子树的根变为整个树的根，然后让其右子树指向之前的根
//结点高度更新操作
rchild->height = MaxHeight(rchild);
root->height = MaxHeight(root);
//返回新的根
return rchild;
}
实际上我们说对某一个结点做RR旋的话，其实就是想将那个结点 往左旋转
3.3.3 LR旋转¶
-
发生情况： 这里的
LR指的是指通过在最低失去平衡的结点的左子树的右子树插入结点，导致失衡所要做出的旋转，当然若是失衡结点的右子树结点被删除也有可能造成LR旋转，因为就“等同左子树的右子树插入结点” -
操作： 当发生
LR失衡的时候，我们可以简单将这颗 \(AVL\) 抽象成如下图所示：
我们需要做一次 RR单旋转以及一次LL单旋，对于上面的情况，我们需要先对 \(k1\) 结点做一次RR单旋，然后再对 \(k3\) 做一次LL单旋，这样就能让二叉树重归平衡
那么步骤的话就可以简化为三步啦（因为之前实现了简单的结点LL右旋和RR左旋操作）
- ①将失衡结点（ \(k3\) ）的左子树结点（ \(k1\) ）RR左旋
- ②将失衡结点（ \(k3\) ）LL右旋
- ③将新的根节点（ \(k2\) ）返回
比如插入序列为：\(\{6,7,2,1,4,3,5 \}\) 的时候，此时以 \(6\) 为根节点的位置的左子树发生了失衡，然后我们对以 \(2\) 为根的左子树进行 RR左旋转然后再对根结点 \(6\) 进行 LL 右旋 如下图所示：
实现代码如下：
template<typename T>
AvlNode<T>* AvlTree<T>::LeftRightRotate(AvlNode<T> *root) {
root->left = RightRightRotate(root->left);//先对左子树进行进行RR旋转
root = LeftLeftRotate(root);//然后对根节点进行LL旋转
return root;//返回新的根
}
3.3.4 RL旋转¶
-
发生情况： 这里的
RL指的是指通过在最低失去平衡的结点的右子树的左子树插入结点，导致失衡所要做出的旋转，当然若是失衡结点的左子树结点被删除也有可能造成LR旋转，因为就“等同右子树的左子树插入结点” -
操作： 当发生
RL失衡的时候，我们可以简单将这颗 \(AVL\) 抽象成如下图所示：
我们需要做一次 LL单旋转以及一次RR单旋，对于上面的情况，我们需要先对 \(k3\) 结点做一次LL单旋，然后再对 \(k1\) 做一次RR单旋，这样就能让二叉树重归平衡
那么步骤的话同样分为三步啦（因为之前实现了简单的结点LL右旋和RR左旋操作）
- ①将失衡结点（ \(k1\) ）的右子树结点（ \(k3\) ）LL 右旋
- ②将失衡结点（ \(k1\) ）LL左旋
- ③将新的根节点（ \(k2\) ）返回
比如插入序列为：\(\{2,1,6,7,4,3,5 \}\) 的时候，此时以 \(2\) 为根节点的位置的右子树发生了失衡，然后我们对以 \(6\) 为根的右子树进行 LL右旋转然后再对根结点 \(2\) 进行 RR 左旋 如下图所示：
代码如下：
template<typename T>
AvlNode<T>* AvlTree<T>::RightLeftRotate(AvlNode<T> *root) {
root->right = LeftLeftRotate(root->right);//先对右子树进行进行LL旋转
root = RightRightRotate(root);//然后对根节点进行LL旋转
return root;//返回新的根
}
3.4 插入操作¶
插入操作其实和正常的二叉搜索树是相同的，还是不断地根据访问到的分支节点与我们插入的结点的值进行比较，若是前者较大，则插入左子树，否则插入右子树，直到我们到达的结点为空，那么此时就完成结点的插入了
前面也提到了结点的插入可能会造成树的失衡，那么我们只需要再回溯根节点的时候不断地向上判断每一个分支节点，看其是否失衡，若是失衡，那么就顺便进行旋转操作（当然若是单独地将检查是否需要旋转操作写成一个函数也是可以的）
于是我们就得到了如下的代码（若是不懂可以看注释）：
template<typename T>
AvlNode<T>* AvlTree<T>::InsetNode(AvlNode<T> *root,T value) {
if(root == NULL) {
root = new AvlNode<T>(value);
} else if(root->key > value) {//插入左子树
root->left = InsetNode(root->left,value);
if(Check_Balance(root->left,root->right)) {//插入左子树后发现失去平衡
if(value < root->left->key) //因为插入结点左子树的左子树上，所以进行LL旋转
root = LeftLeftRotate(root);
else //插入结点在左子树的右子树上，所以LR旋转
root = LeftRightRotate(root);
}
} else {//插入右子树
root->right = InsetNode(root->right,value);
if(Check_Balance(root->right,root->left)) {//插入右子树后发现失去平衡
if(value < root->right->key)//因为插入结点右子树的左子树上，所以进行RL旋转
root = RightLeftRotate(root);
else //因为插入结点右子树的右子树上，所以进行RR旋转
root = RightRightRotate(root);
}
}
root->height = MaxHeight(root);//计算结点高度
return root;
}
3.5 删除操作¶
删除操作这里稍微有一点需要理清逻辑，首先我们肯定还是像二叉排序树一样，不断通过和分支节点比较找到删除的结点的位置，找到节点后我们大体需要分为两种情况：
- 一、若被删除的结点左右子树都不为空
- 若左子树比右子树高（分为三步进行）：
- ①找到当前结点的左子树的最大值结点（前驱）
- ②将这个左子树的最大值赋给当前的根节点
- ③删除左子树的最大值的结点
- 若右子树比左子树高（分为三步进行）：
- ①找到当前结点的右子树上的最小值结点 （后继）
- ②将这个右子树的最小值赋给当前的根节点
- ③删除右子树的最小值结点
- 若左子树比右子树高（分为三步进行）：
- 二、若被删除的结点只有左子树或右子树或者没有左右子树
- 若是只有左子树，那么让其左子树根结点继承当前位置，然后删除该结点
- 若是只有右子树，那么让其右子树根结点继承当前位置，然后删除该结点
- 若是没有左右子树，直接删除该结点
同样的，在结点删除之后二叉树的结构仍然可能会失衡，于是我们需要在递归的归的过程中进行结点平衡判断，于是得到如下代码：
template<typename T>
AvlNode<T>* AvlTree<T>::DeleteNode(AvlNode<T> *root, AvlNode<T> *node) {
if(root == NULL) return NULL;
if(root->key == node->key) { //找到了删除的结点
if(root->left != NULL && root->right != NULL) {
//如果删除的结点的左树和右子树都不为空
if(GetHeight(root->left) > GetHeight(root->right)) {
//如果左子树比右子树高的话，分三步进行
//一、找到当前结点的左子树的最大值结点
AvlNode<T> *max_node = MaxNode(root->left);
//二、将这个左子树的最大值赋给当前的根节点
root->key = max_node->key;
//三、删除左子树的最大值的结点（因为这个结点一定是只有左子树或者没有左子树的情况）
root->left = DeleteNode(root->left,max_node);
} else {
//右子树和左子树更高或者相等,同样分三步
//一、找到当前结点的右子树上的最小值结点
AvlNode<T> *min_node = MinNode(root->right);
//二、将这个右子树的最小值赋给当前的根节点
root->key = min_node->key;
//三、删除右子树的最小值结点（和上面同理，一定是一个只有右子树或者没有右子树的情况）
root->right = DeleteNode(root->right,min_node);
}
} else {//左右子树都为空，或者是左子树为空，或者是右子树为空
AvlNode<T> *tmp = root;//记录下删除的结点
if(root->left == NULL) //如果左子树为空，那么就由右子树继承（当然右子树也可能是一个空树）
root = root->right;
else //否则左子树继承
root = root->left;
delete tmp;
}
}
else if(root->key > node->key) {//删除的结点在左节点
root->left = DeleteNode(root->left,node);
if(Check_Balance(root->right,root->left)) {//右子树可能会失衡
AvlNode<T> *TempRightNode = root->right;
if(GetHeight(TempRightNode->left) > GetHeight(TempRightNode->right))
root = RightLeftRotate(root);//RR旋
else
root = RightRightRotate(root);//RL旋
}
} else {//删除的结点在右子树
root->right = DeleteNode(root->right,node);
if(Check_Balance(root->left,root->right)) {//左子树可能会发生失衡
AvlNode<T> *TempLeftNode = root->left;
if(GetHeight(TempLeftNode->left) > GetHeight(TempLeftNode->right))
root = LeftLeftRotate(root);//LL旋
else
root = LeftRightRotate(root);//LR旋
}
}
if(root)
root->height = MaxHeight(root);
return root;
}
四、完整代码¶
ps：这里的注释可能没有前面的全~
#include<cstring>
#include<iostream>
#include<algorithm>
template<typename T>
class AvlNode {
public:
T key;
int height;
AvlNode *left,*right;
AvlNode(int key) {
this->key = key;
this->height = 0;
this->left = this->right = NULL;
}
~AvlNode() {
}
};
template<typename T>
class AvlTree {
public:
AvlNode<T> *root;
AvlTree() {
this->root = NULL;
}
//获取树结点的高度
int GetHeight(AvlNode<T> *root) {
if(root != NULL)
return root->height;
return 0;
}
//更新树结点的高度
int MaxHeight(AvlNode<T> *root) {
if(root == NULL) return 0;
return std::max(GetHeight(root->left),GetHeight(root->right)) + 1;
}
//判断是否失去平衡
bool Check_Balance(AvlNode<T> *a, AvlNode<T> *b) {
return abs(GetHeight(a) - GetHeight(b)) == 2;
}
/*
这部分完善AVL的左旋、右旋、左右旋、右左旋
*/
//简称为LL旋转（LL的含义是左子树的左子树插入新结点）
AvlNode<T>* LeftLeftRotate(AvlNode<T> *root) {
AvlNode<T> *lchild = root->left;//记录一下左子树根结点
root->left = lchild->right;//将左子树的右子树变为根的左子树
lchild->right = root;//将左子树的根变为整个子树的根，然后让其右子树指向之前的根
//更新一下当前子树的根结点的高height
lchild->height = MaxHeight(lchild);
//更新一下被旋下去的结点，即当前子树的根的右子树结点的高height
root->height = MaxHeight(root);
return lchild;//返回子树旋转后的新的根
}
//简称为RR旋转（RR的含义是右子树的右子树插入新结点）
AvlNode<T>* RightRightRotate(AvlNode<T> *root) {
AvlNode<T> *rchild = root->right;
root->right = rchild->left;
rchild->left = root;
rchild->height = MaxHeight(rchild);
root->height = MaxHeight(root);
return rchild;
}
AvlNode<T>* LeftRightRotate(AvlNode<T> *root) {
root->left = RightRightRotate(root->left);//先对左子树进行进行RR旋转
root = LeftLeftRotate(root);//然后对根节点进行LL旋转
return root;
}
AvlNode<T>* RightLeftRotate(AvlNode<T> *root) {
root->right = LeftLeftRotate(root->right);//先对右子树进行进行LL旋转
root = RightRightRotate(root);//然后对根节点进行LL旋转
return root;
}
//在AVL树中查找元素值为value的结点
AvlNode<T>* ValueFind(AvlNode<T> *root,T value) {
while(root != NULL && root->key != value) {
if(root->key > value) root = root->left;//在左子树
else root = root->right;//在右子树
}
return root;//没找到的话会返回NULL
}
AvlNode<T>* MinNode(AvlNode<T> *root) {
if(root == NULL) return NULL;//特判一下空树的情况
if(root->left == NULL) return root;
return MinNode(root->left);
}
AvlNode<T>* MaxNode(AvlNode<T> *root) {
if(root == NULL) return NULL;//特判一下空树的情况
if(root->right == NULL) return root;
return MaxNode(root->right);
}
//在AVL树中插入元素值为T的结点
AvlNode<T>* InsetNode(AvlNode<T> *root,T value) {
if(root == NULL) {
root = new AvlNode<T>(value);
} else if(root->key > value) {//插入左子树
root->left = InsetNode(root->left,value);
if(Check_Balance(root->left,root->right)) {//插入左子树后发现失去平衡
if(value < root->left->key) //因为插入结点左子树的左子树上，所以进行LL旋转
root = LeftLeftRotate(root);
else //插入结点在左子树的右子树上，所以LR旋转
root = LeftRightRotate(root);
}
} else {//插入右子树
root->right = InsetNode(root->right,value);
if(Check_Balance(root->right,root->left)) {//插入右子树后发现失去平衡
if(value < root->right->key)//因为插入结点右子树的左子树上，所以进行RL旋转
root = RightLeftRotate(root);
else //因为插入结点右子树的右子树上，所以进行RR旋转
root = RightRightRotate(root);
}
}
root->height = MaxHeight(root);//计算结点高度
return root;
}
//删除结点
AvlNode<T>* DeleteNode(AvlNode<T> *root, AvlNode<T> *node) {
if(root == NULL) return NULL;
if(root->key == node->key) { //找到了删除的结点
if(root->left != NULL && root->right != NULL) {
//如果删除的结点的左树和右子树都不为空
if(GetHeight(root->left) > GetHeight(root->right)) {
//如果左子树比右子树高的话，分三步进行
//一、找到当前结点的左子树的最大值结点
AvlNode<T> *max_node = MaxNode(root->left);
//二、将这个左子树的最大值赋给当前的根节点
root->key = max_node->key;
//三、删除左子树的最大值的结点（因为这个结点一定是只有左子树或者没有左子树的情况）
root->left = DeleteNode(root->left,max_node);
} else {
//右子树和左子树更高或者相等,同样分三步
//一、找到当前结点的右子树上的最小值结点
AvlNode<T> *min_node = MinNode(root->right);
//二、将这个右子树的最小值赋给当前的根节点
root->key = min_node->key;
//三、删除右子树的最小值结点（和上面同理，一定是一个只有右子树或者没有右子树的情况）
root->right = DeleteNode(root->right,min_node);
}
} else {//左右子树都为空，或者是左子树为空，或者是右子树为空
AvlNode<T> *tmp = root;//记录下删除的结点
if(root->left == NULL) //如果左子树为空，那么就由右子树继承（当然右子树也可能是一个空树）
root = root->right;
else //否则左子树继承
root = root->left;
delete tmp;
}
}
else if(root->key > node->key) {//删除的结点在左节点
root->left = DeleteNode(root->left,node);
if(Check_Balance(root->right,root->left)) {//右子树可能会失衡
AvlNode<T> *TempRightNode = root->right;
if(GetHeight(TempRightNode->left) > GetHeight(TempRightNode->right))
root = RightLeftRotate(root);//RR旋
else
root = RightRightRotate(root);//RL旋
}
} else {//删除的结点在右子树
root->right = DeleteNode(root->right,node);
if(Check_Balance(root->left,root->right)) {//左子树可能会发生失衡
AvlNode<T> *TempLeftNode = root->left;
if(GetHeight(TempLeftNode->left) > GetHeight(TempLeftNode->right))
root = LeftLeftRotate(root);//LL旋
else
root = LeftRightRotate(root);//LR旋
}
}
if(root)
root->height = MaxHeight(root);
return root;
}
//先序遍历
void PreOrder(AvlNode<T> *root) {
if(root == NULL) return;
std::cout<<root->key<<"->";
PreOrder(root->left);
PreOrder(root->right);
}
//中序遍历
void InOrder(AvlNode<T> *root) {
if(root == NULL) return;
InOrder(root->left);
std::cout<<root->key<<"->";
InOrder(root->right);
}
//后序遍历
void PostOrder(AvlNode<T> *root) {
if(root == NULL) return;
PostOrder(root->left);
PostOrder(root->right);
std::cout<<root->key<<"->";
}
};
int main()
{
AvlTree<int> * Tree = new AvlTree<int>();
int n = 8;
for(int i = 1;i <= n; ++i) {
Tree->root = Tree->InsetNode(Tree->root,i);
std::cout<<"-----------"<<std::endl;
std::cout<<"先序遍历为："<<std::endl;
Tree->PreOrder(Tree->root);
std::cout<<"\n中序遍历为："<<std::endl;
Tree->InOrder(Tree->root);
std::cout<<std::endl;
}
std::cout<<"hello"<<std::endl;
AvlNode<int> *p = Tree->ValueFind(Tree->root,5);
Tree->DeleteNode(Tree->root,p);
std::cout<<"-----------"<<std::endl;
std::cout<<"先序遍历为："<<std::endl;
Tree->PreOrder(Tree->root);
std::cout<<"\n中序遍历为："<<std::endl;
Tree->InOrder(Tree->root);
return 0;
}
/*
output：
-----------
先序遍历为：
1->
中序遍历为：
1->
-----------
先序遍历为：
1->2->
中序遍历为：
1->2->
-----------
先序遍历为：
2->1->3->
中序遍历为：
1->2->3->
-----------
先序遍历为：
2->1->3->4->
中序遍历为：
1->2->3->4->
-----------
先序遍历为：
2->1->4->3->5->
中序遍历为：
1->2->3->4->5->
-----------
先序遍历为：
4->2->1->3->5->6->
中序遍历为：
1->2->3->4->5->6->
-----------
先序遍历为：
4->2->1->3->6->5->7->
中序遍历为：
1->2->3->4->5->6->7->
-----------
先序遍历为：
4->2->1->3->6->5->7->8->
中序遍历为：
1->2->3->4->5->6->7->8->
hello
-----------
先序遍历为：
4->2->1->3->7->6->8->
中序遍历为：
1->2->3->4->6->7->8->
*/
五、应用¶
\(AVL\) 的平衡操作，让二叉排序树更加的稳定，因此我们可以根据这个去实现一些 \(STL\) 之类的容器，例如 map 、set
下面就是一份用 AVL 树实现的 map 容器：
/**
* @brief An AVLTree-based map implementation
* @details The map is sorted according to the natural ordering of its
* keys or by a {@code Compare} function provided; This implementation
* provides guaranteed log(n) time cost for the contains, get, insert
* and remove operations.
*/
#ifndef AVLTREE_MAP_HPP
#define AVLTREE_MAP_HPP
#include <cassert>
#include <cstddef>
#include <cstdint>
#include <functional>
#include <memory>
#include <stack>
#include <utility>
#include <vector>
#include <iostream>
/**
* An AVLTree-based map implementation
* https://en.wikipedia.org/wiki/AVL_tree
* @tparam Key the type of keys maintained by this map
* @tparam Value the type of mapped values
* @tparam Compare
*/
template <typename Key, typename Value, typename Compare = std::less<Key> >
class AvlTreeMap {
private:
using USize = size_t;
using Factor = int64_t;
Compare compare = Compare();
public:
struct Entry {
Key key;
Value value;
bool operator==(const Entry &rhs) const noexcept {
return this->key == rhs.key && this->value == rhs.value;
}
bool operator!=(const Entry &rhs) const noexcept {
return this->key != rhs.key || this->value != rhs.value;
}
};
private:
struct Node {
using Ptr = std::shared_ptr<Node>;
using Provider = const std::function<Ptr(void)> &;
using Consumer = const std::function<void(const Ptr &)> &;
Key key;
Value value{};
Ptr left = nullptr;
Ptr right = nullptr;
USize height = 1;
explicit Node(Key k) : key(std::move(k)) {}
explicit Node(Key k, Value v) : key(std::move(k)), value(std::move(v)) {}
~Node() = default;
inline bool isLeaf() const noexcept {
return this->left == nullptr && this->right == nullptr;
}
inline void updateHeight() noexcept {
if (this->isLeaf()) {
this->height = 1;
} else if (this->left == nullptr) {
this->height = this->right->height + 1;
} else if (this->right == nullptr) {
this->height = this->left->height + 1;
} else {
this->height = std::max(left->height, right->height) + 1;
}
}
inline Factor factor() const noexcept {
if (this->isLeaf()) {
return 0;
} else if (this->left == nullptr) {
return (Factor)this->right->height;
} else if (this->right == nullptr) {
return (Factor) - this->left->height;
} else {
return (Factor)(this->right->height - this->left->height);
}
}
inline Entry entry() const {
return Entry{key, value};
}
static Ptr from(const Key &k) {
return std::make_shared<Node>(Node(k));
}
static Ptr from(const Key &k, const Value &v) {
return std::make_shared<Node>(Node(k, v));
}
};
using NodePtr = typename Node::Ptr;
using ConstNodePtr = const NodePtr &;
using NodeProvider = typename Node::Provider;
using NodeConsumer = typename Node::Consumer;
NodePtr root = nullptr;
USize count = 0;
using K = const Key &;
using V = const Value &;
public:
using EntryList = std::vector<Entry>;
using KeyValueConsumer = const std::function<void(K, V)> &;
using MutKeyValueConsumer = const std::function<void(K, Value &)> &;
using KeyValueFilter = const std::function<bool(K, V)> &;
class NoSuchMappingException : protected std::exception {
private:
const char *message;
public:
explicit NoSuchMappingException(const char *msg) : message(msg) {}
const char *what() const noexcept override {
return message;
}
};
AvlTreeMap() noexcept = default;
/**
* Returns the number of entries in this map.
* @return size_t
*/
inline USize size() const noexcept {
return this->count;
}
/**
* Returns true if this collection contains no elements.
* @return bool
*/
inline bool empty() const noexcept {
return this->count == 0;
}
/**
* Removes all of the elements from this map.
*/
void clear() noexcept {
this->root = nullptr;
this->count = 0;
}
/**
* Returns the value to which the specified key is mapped; If this map
* contains no mapping for the key, a {@code NoSuchMappingException} will
* be thrown.
* @param key
* @return AvlTreeMap<Key, Value>::Value
* @throws NoSuchMappingException
*/
Value get(K key) const {
if (this->root == nullptr) {
throw NoSuchMappingException("Invalid key");
} else {
NodePtr node = this->getNode(this->root, key);
if (node != nullptr) {
return node->value;
} else {
throw NoSuchMappingException("Invalid key");
}
}
}
/**
* Returns the value to which the specified key is mapped; If this map
* contains no mapping for the key, a new mapping with a default value
* will be inserted.
* @param key
* @return AvlTreeMap<Key, Value>::Value &
*/
Value &getOrDefault(K key) {
if (this->root == nullptr) {
this->root = Node::from(key);
this->count += 1;
return this->root->value;
} else {
return this
->getNodeOrProvide(this->root, key,
[&key]() {
return Node::from(key);
})
->value;
}
}
/**
* Returns true if this map contains a mapping for the specified key.
* @param key
* @return bool
*/
bool contains(K key) const {
return this->getNode(this->root, key) != nullptr;
}
/**
* Associates the specified value with the specified key in this map.
* @param key
* @param value
*/
void insert(K key, V value) {
if (this->root == nullptr) {
this->root = Node::from(key, value);
this->count += 1;
} else {
this->insert(this->root, key, value);
}
}
/**
* If the specified key is not already associated with a value, associates
* it with the given value and returns true, else returns false.
* @param key
* @param value
* @return bool
*/
bool insertIfAbsent(K key, V value) {
USize sizeBeforeInsertion = this->size();
if (this->root == nullptr) {
this->root = Node::from(key, value);
this->count += 1;
} else {
this->insert(this->root, key, value, false);
}
return this->size() > sizeBeforeInsertion;
}
/**
* If the specified key is not already associated with a value, associates
* it with the given value and returns the value, else returns the associated
* value.
* @param key
* @param value
* @return
*/
Value &getOrInsert(K key, V value) {
if (this->root == nullptr) {
this->root = Node::from(key, value);
this->count += 1;
return root->value;
} else {
NodePtr node = getNodeOrProvide(this->root, key,
[&]() {
return Node::from(key, value);
});
return node->value;
}
}
Value operator[](K key) const {
return this->get(key);
}
Value &operator[](K key) {
return this->getOrDefault(key);
}
/**
* Removes the mapping for a key from this map if it is present;
* Returns true if the mapping is present else returns false
* @param key the key of the mapping
* @return bool
*/
bool remove(K key) {
if (this->root == nullptr) {
return false;
} else {
return this->remove(this->root, key, [](ConstNodePtr) {});
}
}
/**
* Removes the mapping for a key from this map if it is present and returns
* the value which is mapped to the key; If this map contains no mapping for
* the key, a {@code NoSuchMappingException} will be thrown.
* @param key
* @return AvlTreeMap<Key, Value>::Value
* @throws NoSuchMappingException
*/
Value getAndRemove(K key) {
Value result;
NodeConsumer action = [&](ConstNodePtr node) {
result = node->value;
};
if (root == nullptr) {
throw NoSuchMappingException("Invalid key");
} else {
if (remove(this->root, key, action)) {
return result;
} else {
throw NoSuchMappingException("Invalid key");
}
}
}
/**
* Gets the entry corresponding to the specified key; if no such entry
* exists, returns the entry for the least key greater than the specified
* key; if no such entry exists (i.e., the greatest key in the Tree is less
* than the specified key), a {@code NoSuchMappingException} will be thrown.
* @param key
* @return AvlTreeMap<Key, Value>::Entry
* @throws NoSuchMappingException
*/
Entry getCeilingEntry(K key) const {
if (this->root == nullptr) {
throw NoSuchMappingException("No ceiling entry in this map");
}
NodePtr node = this->root;
std::stack<NodePtr> ancestors;
while (node != nullptr) {
if (key == node->key) {
return node->entry();
}
if (compare(key, node->key)) {
/* key < node->key */
if (node->left != nullptr) {
ancestors.push(node);
node = node->left;
} else {
return node->entry();
}
} else {
/* key > node->key */
if (node->right != nullptr) {
ancestors.push(node);
node = node->right;
} else {
if (ancestors.empty()) {
throw NoSuchMappingException("No ceiling entry in this map");
}
NodePtr parent = ancestors.top();
ancestors.pop();
while (node == parent->right) {
node = parent;
if (!ancestors.empty()) {
parent = ancestors.top();
ancestors.pop();
} else {
throw NoSuchMappingException("No ceiling entry in this map");
}
}
return parent->entry();
}
}
}
throw NoSuchMappingException("No ceiling entry in this map");
}
/**
* Gets the entry corresponding to the specified key; if no such entry exists,
* returns the entry for the greatest key less than the specified key;
* if no such entry exists, a {@code NoSuchMappingException} will be thrown.
* @param key
* @return AvlTreeMap<Key, Value>::Entry
* @throws NoSuchMappingException
*/
Entry getFloorEntry(K key) const {
if (this->root == nullptr) {
throw NoSuchMappingException("No floor entry exists in this map");
}
NodePtr node = this->root;
std::stack<NodePtr> ancestors;
while (node != nullptr) {
if (key == node->key) {
return node->entry();
}
if (compare(key, node->key)) {
/* key < node->key */
if (node->left != nullptr) {
ancestors.push(node);
node = node->left;
} else {
if (ancestors.empty()) {
throw NoSuchMappingException("No floor entry exists in this map");
}
NodePtr parent = ancestors.top();
ancestors.pop();
while (node == parent->left) {
node = parent;
if (!ancestors.empty()) {
parent = ancestors.top();
ancestors.pop();
} else {
throw NoSuchMappingException("No floor entry exists in this map");
}
}
return parent->entry();
}
} else {
/* key > node->key */
if (node->right != nullptr) {
ancestors.push(node);
node = node->right;
} else {
return node->entry();
}
}
}
throw NoSuchMappingException("No floor entry exists in this map");
}
/**
* Gets the entry for the least key greater than the specified
* key; if no such entry exists, returns the entry for the least
* key greater than the specified key; if no such entry exists,
* a {@code NoSuchMappingException} will be thrown.
* @param key
* @return AvlTreeMap<Key, Value>::Entry
* @throws NoSuchMappingException
*/
Entry getHigherEntry(K key) {
if (this->root == nullptr) {
throw NoSuchMappingException("No higher entry exists in this map");
}
NodePtr node = this->root;
std::stack<NodePtr> ancestors;
while (node != nullptr) {
if (compare(key, node->key)) {
/* key < node->key */
if (node->left != nullptr) {
ancestors.push(node);
node = node->left;
} else {
return node->entry();
}
} else {
/* key >= node->key */
if (node->right != nullptr) {
ancestors.push(node);
node = node->right;
} else {
if (ancestors.empty()) {
throw NoSuchMappingException("No higher entry exists in this map");
}
NodePtr parent = ancestors.top();
ancestors.pop();
while (node == parent->right) {
node = parent;
if (!ancestors.empty()) {
parent = ancestors.top();
ancestors.pop();
} else {
throw NoSuchMappingException(
"No higher entry exists in this map");
}
}
return parent->entry();
}
}
}
throw NoSuchMappingException("No higher entry exists in this map");
}
/**
* Returns the entry for the greatest key less than the specified key; if
* no such entry exists (i.e., the least key in the Tree is greater than
* the specified key), a {@code NoSuchMappingException} will be thrown.
* @param key
* @return AvlTreeMap<Key, Value>::Entry
* @throws NoSuchMappingException
*/
Entry getLowerEntry(K key) const {
if (this->root == nullptr) {
throw NoSuchMappingException("No lower entry exists in this map");
}
NodePtr node = this->root;
std::stack<NodePtr> ancestors;
while (node != nullptr) {
if (compare(key, node->key) || key == node->key) {
/* key <= node->key */
if (node->left != nullptr) {
ancestors.push(node);
node = node->left;
} else {
if (ancestors.empty()) {
throw NoSuchMappingException("No lower entry exists in this map");
}
NodePtr parent = ancestors.top();
ancestors.pop();
while (node == parent->left) {
node = parent;
if (!ancestors.empty()) {
parent = ancestors.top();
ancestors.pop();
} else {
throw NoSuchMappingException("No lower entry exists in this map");
}
}
return parent->entry();
}
} else {
/* key > node->key */
if (node->right != nullptr) {
ancestors.push(node);
node = node->right;
} else {
return node->entry();
}
}
}
throw NoSuchMappingException("No lower entry exists in this map");
}
/**
* Remove all entries that satisfy the filter condition.
* @param filter
*/
void removeAll(KeyValueFilter filter) {
std::vector<Key> keys;
this->inorderTraversal([&](ConstNodePtr node) {
if (filter(node->key, node->value)) {
keys.push_back(node->key);
}
});
for (const Key &key : keys) {
this->remove(key);
}
}
/**
* Performs the given action for each key and value entry in this map.
* The value is immutable for the action.
* @param action
*/
void forEach(KeyValueConsumer action) const {
this->inorderTraversal(
[&](ConstNodePtr node) {
action(node->key, node->value);
});
}
/**
* Performs the given action for each key and value entry in this map.
* The value is mutable for the action.
* @param action
*/
void forEachMut(MutKeyValueConsumer action) {
this->inorderTraversal(
[&](ConstNodePtr node) {
action(node->key, node->value);
});
}
/**
* Returns a list containing all of the entries in this map.
* @return AvlTreeMap<Key, Value>::EntryList
*/
EntryList toEntryList() const {
EntryList entryList;
this->inorderTraversal(
[&](ConstNodePtr node) {
entryList.push_back(node->entry());
});
return entryList;
}
private:
static NodePtr rotateLeft(ConstNodePtr node) {
// clang-format off
// | |
// N S
// / \ l-rotate(N) / \
// L S ==========> N R
// / \ / \
// M R L M
NodePtr successor = node->right;
// clang-format on
node->right = successor->left;
successor->left = node;
node->updateHeight();
successor->updateHeight();
return successor;
}
static NodePtr rotateRight(ConstNodePtr node) {
// clang-format off
// | |
// N S
// / \ r-rotate(N) / \
// S R ==========> L N
// / \ / \
// L M M R
NodePtr successor = node->left;
// clang-format on
node->left = successor->right;
successor->right = node;
node->updateHeight();
successor->updateHeight();
return successor;
}
static void swapNode(NodePtr &lhs, NodePtr &rhs) {
std::swap(lhs->key, rhs->key);
std::swap(lhs->value, rhs->value);
std::swap(lhs, rhs);
}
static void fixBalance(NodePtr &node) {
if (node->factor() < -1) {
if (node->left->factor() < 0) {
// clang-format off
// Left-Left Case
// |
// C |
// / r-rotate(C) B
// B ==========> / \
// / A C
// A
// clang-format on
node = rotateRight(node);
} else {
// clang-format off
// Left-Right Case
// | |
// C C |
// / l-rotate(A) / r-rotate(C) B
// A ==========> B ==========> / \
// \ / A C
// B A
// clang-format on
node->left = rotateLeft(node->left);
node = rotateRight(node);
}
} else if (node->factor() > 1) {
if (node->right->factor() > 0) {
// clang-format off
// Right-Right Case
// |
// C |
// \ l-rotate(C) B
// B ==========> / \
// \ A C
// A
// clang-format on
node = rotateLeft(node);
} else {
// clang-format off
// Right-Left Case
// | |
// A A |
// \ r-rotate(C) \ l-rotate(A) B
// C ==========> B ==========> / \
// / \ A C
// B C
// clang-format on
node->right = rotateRight(node->right);
node = rotateLeft(node);
}
}
}
NodePtr getNodeOrProvide(NodePtr &node, K key, NodeProvider provide) {
assert(node != nullptr);
if (key == node->key) {
return node;
}
assert(key != node->key);
NodePtr result;
if (compare(key, node->key)) {
/* key < node->key */
if (node->left == nullptr) {
result = node->left = provide();
this->count += 1;
node->updateHeight();
} else {
result = getNodeOrProvide(node->left, key, provide);
node->updateHeight();
fixBalance(node);
}
} else {
/* key > node->key */
if (node->right == nullptr) {
result = node->right = provide();
this->count += 1;
node->updateHeight();
} else {
result = getNodeOrProvide(node->right, key, provide);
node->updateHeight();
fixBalance(node);
}
}
return result;
}
NodePtr getNode(ConstNodePtr node, K key) const {
assert(node != nullptr);
if (key == node->key) {
return node;
}
if (compare(key, node->key)) {
/* key < node->key */
return node->left == nullptr ? nullptr : getNode(node->left, key);
} else {
/* key > node->key */
return node->right == nullptr ? nullptr : getNode(node->right, key);
}
}
void insert(NodePtr &node, K key, V value, bool replace = true) {
assert(node != nullptr);
if (key == node->key) {
if (replace) {
node->value = value;
}
return;
}
assert(key != node->key);
if (compare(key, node->key)) {
/* key < node->key */
if (node->left == nullptr) {
node->left = Node::from(key, value);
this->count += 1;
node->updateHeight();
} else {
insert(node->left, key, value, replace);
node->updateHeight();
fixBalance(node);
}
} else {
/* key > node->key */
if (node->right == nullptr) {
node->right = Node::from(key, value);
this->count += 1;
node->updateHeight();
} else {
insert(node->right, key, value, replace);
node->updateHeight();
fixBalance(node);
}
}
}
bool remove(NodePtr &node, K key, NodeConsumer action) {
assert(node != nullptr);
if (key != node->key) {
if (compare(key, node->key)) {
/* key < node->key */
NodePtr &left = node->left;
if (left != nullptr && remove(left, key, action)) {
node->updateHeight();
fixBalance(node);
return true;
} else {
return false;
}
} else {
/* key > node->key */
NodePtr &right = node->right;
if (right != nullptr && remove(right, key, action)) {
node->updateHeight();
fixBalance(node);
return true;
} else {
return false;
}
}
}
assert(key == node->key);
action(node);
if (node->isLeaf()) {
// Case 1: no child
node = nullptr;
} else if (node->right == nullptr) {
// clang-format off
// Case 2: left child only
// P
// | remove(N) P
// N ========> |
// / L
// L
// clang-format on
node = node->left;
node->updateHeight();
} else if (node->left == nullptr) {
// clang-format off
// Case 3: right child only
// P
// | remove(N) P
// N ========> |
// \ R
// R
// clang-format on
node = node->right;
node->updateHeight();
} else if (node->right->left == nullptr) {
// clang-format off
// Case 4: both left and right child, right child has no left child
// | |
// N remove(N) R
// / \ ========> /
// L R L
// clang-format on
NodePtr right = node->right;
swapNode(node, right);
right->right = node->right;
node = right;
node->updateHeight();
fixBalance(node);
} else {
// clang-format off
// Case 5: both left and right child, right child is not a leaf
// Step 1. find the node N with the smallest key
// and its parent P on the right subtree
// Step 2. swap S and N
// Step 3. remove node N like Case 1 or Case 3
// Step 4. update height for P
// | |
// N S |
// / \ / \ S
// L .. swap(N, S) L .. remove(N) / \
// | =========> | ========> L ..
// P P |
// / \ / \ P
// S .. N .. / \
// \ \ R ..
// R R
// clang-format on
// Step 1
NodePtr successor = node->right;
NodePtr parent = node;
while (successor->left != nullptr) {
parent = successor;
successor = parent->left;
}
// Step 2
swapNode(node, successor);
// Step 3
parent->left = node->right;
// Restore node
node = successor;
// Step 4
parent->updateHeight();
}
this->count -= 1;
return true;
}
void inorderTraversal(NodeConsumer action) const {
if (this->root == nullptr) {
return;
}
std::stack<NodePtr> stack;
NodePtr node = this->root;
while (node != nullptr || !stack.empty()) {
while (node != nullptr) {
stack.push(node);
node = node->left;
}
if (!stack.empty()) {
node = stack.top();
stack.pop();
action(node);
node = node->right;
}
}
}
};
#endif // AVLTREE_MAP_HPP
int main()
{
AvlTreeMap<int,int> vis;
for(int i = 1;i < 10; ++i) {
vis[i] = i * i;
}
for(int i = 1;i <= 100; ++i) {
if(vis[i] == i * i)
std::cout<<"The "<<i<<" Yes"<<std::endl;
}
return 0;
}
/*
output:
The 1 Yes
The 2 Yes
The 3 Yes
The 4 Yes
The 5 Yes
The 6 Yes
The 7 Yes
The 8 Yes
The 9 Yes
*/
最后附上参考的文章：
-
平衡二叉树（AVL树）：https://www.cnblogs.com/sench/p/7786718.html
-
AVL树(二)之 C++的实现 ：https://www.cnblogs.com/skywang12345/p/3577360.html
-
OI Wiki AVL 树：https://oi-wiki.org/ds/avl/
最后更新:
2022-09-06 08:33:20